Dwa różne pierwiatki dodatnie cyaneus: Proszę o pomoc, pewnie coś pominęłam i dlatego nie chce mi wyjść zgodnie z odpowiedziami... Wyznacz wartość parametru m, dla których równanie ma dwa różne pierwiastki dodatnie. x² + (2m−3)x + 2m + 5 = 0 a≠0 Δ>0 −(b/a)>0 c/a>0 Δ=(2m−3)² − 4(2m+5) Δ=(4m² − 12m + 9) − 8m − 20 Δ=4m² − 20m − 11 Δ=400 − 4(−11)4 Δ=576 m₁=−(1/2) m₂=5 1/2 m∊(−∞, −(1/2) ) u (5 1/2, ∞) − (2m+3)/1 >0 m> − 3/2 czyli m∊(−3/2, −1/2) u (5 1/2, ∞) W podręczniku za to wychodzi m ∊ (−5/2, −1/2).

Atar1x: a drugi warunek że x₁+x₂>0 bo na razie masz pokazane ze oba sa tego samego znaku

Technik: a≠0 Δ>0 x₁*x₂>0 x₁+x₂>0 Δ=(2m−3)²−4(2m+5) Δ=4m²−12m+9−8m−20 Δ=4m²−20m−11 Δ_m=(−20)²−4*4*(−11)=576 √Δ_m=24

	20−24		1
m1=		=−
	8		2

	20+24		1
m2=		=5
	8		2

	1		1
m∊(−∞,−		)∪(5		,∞)
	2		2

x₁*x₂>0

2m+5
	>0
1

2m+5>0 2m>−5 /2

	5
m>−
	2

	5
m∊(−		,∞)
	2

x₁+x₂>0

	b
−		>0
	a

−(2m−3
	>0
1

−2m+3>0 −2m>−3 2m<3/2

	3
m<
	2

	3
m∊(−∞,		)
	2

cyaneus: Aaaa podzieliłam samą piątkę przez jedynkę w tym drugim... tak więc wychodzi m>−5/2. Ale dlaczego tylko do −1/2?

Technik: weź cześć wspólną tych przedziałów

Kejt: chodzi Ci o metodę czy rachunkowo?

Technik: Metoda jest dobra chyba ja innej nie znam ale zobacz czy nie ma błędu w obliczeniach (pierwszy raz w życiu robiłem tego typu zadanie )

cyaneus: Narysowałam sobie te przedziały, no i dla mnie część wspólna to właśnie moja niezgadzająca się odpowiedź... No bo jeśli m ma ustalone tylko "od" to ten drugi przedział z warunku delty też pasuje

Kejt: taa..zobacz czy nie ma błędu.. z moim dzisiejszym geniuszem

Kejt: jeśli masz dobre wzory Viete'a to wg mnie rachunkowo jest w porządku..

Technik: im bliżej matury tym coraz gorzej odpoczywaj teraz

Kejt: o nie, nie.. jak nie skończę planimetrii, kombinatoryki i prawdopodobieństwa..to nie będę mogła spać po nocach..

Technik: ja teraz powtarzam tylko słówka na angielki i pisze jakieś recenzje i różne pierdoły....

Kejt: za angielski się jeszcze nie wzięłam ale z tym nie mam jakichś szczególnych problemów..

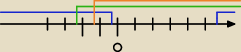
cyaneus: Tylko co z tą częścią wspólną Ja tej z odp nie widze... Tak, im bliżej matury tym coraz więcej błędów

Technik: jeden błąd jednej literki zapomnisz i tracisz już punkt

Kejt: proponuję wrzucić do wolframa i sprawdzić, czy nierówności są dobrze rozwiązane..

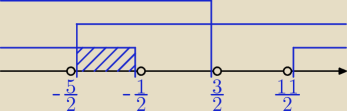
Bogdan: To jeszcze raz. x² + (2m − 3)x + 2m + 5 = 0, a = 1, 2m − 3 = 0, c = 2m + 5 Założenia:

	1		11
1) Δ > 0 ⇒ 4m2 − 20m − 1 > 0 ⇒ m < −		lub x >
	2		2

	c		5
2) x1 * x2 > 0 ⇒		> 0 ⇒ 2m + 5 > 0 ⇒ m > −
	a		2

	−b		3
3) x1 + x2 > 0 ⇒		> 0 ⇒ −2m + 3 > 0 ⇒ m <
	a		2

	5		1
Rozwiązanie widać na rysunku: x ∊ (−		, −		)
	2		2

cyaneus: Już wszystko jasne! W 3 założeniu pomieszałam znaki... Dziękuje bardzo za pomoc

Technik: Czyli moje obliczenia były poprawne

Kejt: czyli ja się nie pomyliłam przy sprawdzaniu