prooooosze :( kk: proooosze o pomoc.. kompetnie nie mam pomysłu jak zrobić Punkt A (1,2√3) jest wierzchołkiem trójkąta równobocznego ABC. Bok BC jest zawarty w prostej o równaniu 3y=√3x− √3 . Oblicz B, C

rav668: o to jest dobre zadanko

rav668: Dobrą masz tą funkcję? Bo na moje oko to tam nie ma odcinka prostego (takiego, który mógłby być bokiem trójkąta), chyba że tylko ja nie widze.

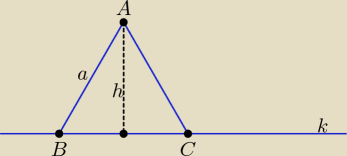
Bogdan: Wyznacz h, potem a, następnie równanie okręgu o środku A i promieniu a. Wreszcie rozwiąż układ równań: równanie tego okręgu i równanie prostej k.

rav668: Można policzyć ze wzoru na odległość punktu od prostej. Wtedy odległość A od prostej będzie wysokością trójkąta. Następnie obliczyć bok a i zaznaczyć na prostej prostopadłej do wysokości punkty odległe o a/2 i mamy B i C

Bogdan: "i zaznaczyć na prostej prostopadłej do wysokości punkty odległe o a/2 i mamy B i C" − sprecyzuj rav668 to działanie

rav668: Znając wzór prostej prostopadłej, znamy kąt pod jakim jest nachylona do osi OX. Naszą przeciwprostokątną jest a/2, wiec mozemy z pitagorasa wyliczyć wektor przesunięcia "i mamy B i C" . Coś takiego mi chodzi po głowie, ale proszę o korekcję jeśli coś się nie zgadza. Pozdrawiam.

Michał: @rav668 no tutaj bym sie wahał z twoim sposobem. robiłem to zadanie ostatnio i tak jak Bogdan podpowiada z tym okręgiem jest najłatwiej

Bogdan: Wykonaj rav668 te obliczenia na kartce i sprawdź, czy Twoja propozycja da w prosty sposób rozwiązanie i czy w ogóle da rozwiązanie.