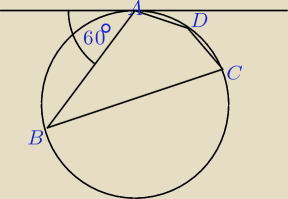
W okrąg o promieniu r wpisano czworokąt ABCD taki, że kąt Domislaw: W okrąg o promieniu r wpisano czworokąt ABCD taki, że kąt między styczną poprowadzoną do okręgu w punkcie A i Bokiem AB ma miarę 60^o. wyznacz pole czworokąta ABCD, jeśli |BC| = 2|AC| oraz |AD| =|DC|. Znalazlem na innych stronach rozwiazanie w ktorym załozono ze kat BAC jest prosty i powolywano sie na twierdzenie o kacie miedzy styczna a cieciwa, nie widze tego, prosze o pomoc.

Basia: trzeba skorzystać z twierdzenia o kącie dopisanym wynika z niego, że |∡BCA| = 60^o i wtedy z tego, że |BC| = 2|AC| masz AB² = AC² + BC² − 2AC*BC*cos60

	1
AB2 = AC2 + 4AC2 − 4AC2*		= 3AC2
	2

stąd BC² = (2AC)² = 4AC² = 3AC²+AC² = AB²+AC² na mocy tw. odwrotnego do tw.Pitagorasa ∡BAC = 90^o