Dzień dobry 
Mam problem z ruszeniem z zadaniem.
W treści mam: W trójkącie ABC środkowa opuszczona z wierzchołka C jest dwa razy krótsza od boku
AB. Wyznacz miarę kąta ACB.
Szukałem takiego zadania w google, znalazłem jedną podpowiedź, ale błędną.
Tak więc zaczynam od tego co wiem:
1. Rysuję trójkąt ABC, środkową d oraz kąt α.
2. Wiem, że |CO| jest 2 razy krótsze od |AB|.
I dalej naprawdę nie wiem, a odpowiedź wynosi 90 stopni.
Czy byłby ktoś miły pomóc w tym zadaniu? Pozdrawiam
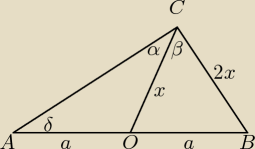
| x | a | ||
= | |||
| sin(δ) | sin(α) |
| 2x | 2a | ||
= | |||
| sin(δ) | sin(α+β) |
dziękuje.
Tylko kwestia oznaczeń, bo |AB| jest 2x, ramiona są nieznane
nie to wtedy tak:
A jest srodkiem okregu opisanego na trojkacie o promieniu x
przy wierzcholku A musi byc kat prosty
@yep