równanie z parametem p: Dla jakich wartości parametru a jeden z pierwiastków równania: (2a+1)x² − ax + a −2 = 0 jest większy od 1, a drugi mniejszy od 1? policzyłam Δ i wyszło, że a ∊ ((6−2√23)/7 ; (6+2√23)/7 ) Tylko nie wiem co dalej z tym zrobić

p: podbijam

pigor: ..., a więc np. tak : niech f(x)= (2a+1)x²−ax+a−2, to warunki zadania spełnia układ nierówności : Δ=a²−4(2a+1)(a−2)>0 i (2a+1)* f(1)<0 ⇔ a²−8a²+12a+8>0 i (2a+1)(2a+1−a+a−2)<0 ⇔ ⇔ −7a²+12a+8>0 /*(−1) i (2a+1)(2a−1)<0 ⇔ 7a²−12a−8<0 i 4a²−1<0 ⇒ ⇒ 7a²−12a−8< 0 i √Δ_a=4√23 i a²<¹₄ ⇒ ⇒ −¹₇(6−2√23)< a< ¹₇{6+2√23) i |a|< ¹₂ ⇒ ⇒ około −0,51< a< 2,2 i −¹₂< a < ¹₂ ⇒ −¹₂< a < ¹₂ ⇔ ⇔ a∊(−¹₂ ; ¹₂) − szukany zbiór wartości parametru a . ...

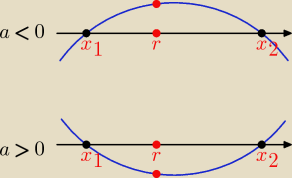
Bogdan: Jeśli liczba r zawarta jest w przedziale (x₁, x₂), gdzie x₁, x₂ to pierwiastki równania ax² + bx + c = 0, to przyjmujemy założenia: 1) a ≠ 0 2) Δ > 0 3) a*f(r) < 0 Rozwiązaniem jest część wspólna rozwiązań tych nierówności.

Dominik:

	−b
a nie lepiej a ≠ 0 ∧ Δ > 0 ∧		= 1? strasznie kombinujecie albo ja zle rozumiem
	2a

polecenie.

pigor: ...., ty Dominik swoimi warunkami rozpatrujesz tylko 1 przypadek, a nie "wszystkie". a u Bogdan−a , punkt 1) nie jest konieczny, bo punkt 3) zapewnia go . ...

Dominik: wciaz nie rozumiem. moglbys mi podac przyklad funkcji kwadratowej, ktora spelnia warunki zadania, a nie ma wspolrzednej x wierzcholka rownej 1?

Dominik: dobra, rozumiem. wasze rozwiazania sa jak najbardziej poprawne.

pigor: ... , dziękuję . ...

sinus: ja mam pytanie co nam daje to założenie b*f(1) < 0 , b − współczynnik kierunkowy (2a+1)*f(1) < 0 ? bo zastanawiam sie juz od dłuzszego czasu i nic nie moge wymyslić

sinus: albo inaczej co było by w przypadku gdyby (2a+1)*f(1) > 0 ?

sinus: ?

sinus: bardzo prosze o wyjaśnienie

sinus: pomoże ktoś?