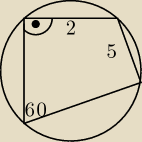
Wielokąty bednarz: Czworokąt jest opisany na okręgu. Wyznacz jego promień

CAROLINE: TEN CZWOROKĄT JEST WPISANY W OKRĄG

Dominik: ten czworokat jest prostokatem (dlaczego?)

bednarz: Sory za błąd, czworokąt wpisany w okrąg

bednarz: nie jest prostokątem, bo ma miary kątów 90, 90, 60 i 120

Dominik: racja pospieszylem sie

CAROLINE: a jakby poprowadzić przekątną z tego kąta 60 do przeciwległego? i potem powyliczać z Pitagorasa?

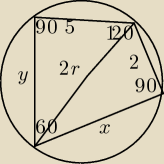
bednarz: Tyle wiem na pewno. I WAŻNE − na pierwszym rysunku źle zaznaczyłem długości boków, teraz jest dobrze

bednarz: do pitagorasa brakuje mi jednej danej, może coś policzyć z tw sinusów, lub cosinusów, tylko nie wiem, w jaki sposób ta przekątna dzieli kąty, bo na pewno nie na pół

bednarz: Hej maturzyści! Nikt nie wie?

Aga1.: Wykorzystać twierdzenie cosinusów do obliczenia przekątnej wychodzącej z wierzchołków kątów 90⁰. x²=2²+5²−2*2*5*cos120⁰ A teraz z twierdzenia sinusów

x
	=2R., gdzie R to promień okręgu opisanego na czworokącie.
sin600

Ania_601:

	√64−10√39
A więc ja policzyłam, tylko r mi wyszło dziwne torche.. r=
	2

Ania_601: ja zauważyłam, że ta druga przekątna, którą obliczymy z twierdzenia cosinusów dzieli te kąty 90 na 60 i 30 więc mamy tam trójkąt równoboczny więc y jest równy tyle samo co ta przekątna i wtedy wyliczamy r znowu z twierdzenia cosinusów

bednarz: r powinien wyjść √13, Ania₆01, wyszło Ci tak?

bednarz: ale dlaczego je dzieli na 60 i 30, jak to wywnioskowałas?