ostrosłup prawidłowy trójkatny
duo: Krawędź boczna ostrosłupa prawidłowego trójkątnego ma długość 2√7. Ściana boczna tego
ostrosłupa jest nachylona do płaszczyzny podstawy pod katem 60 stopni . Oblicz tg kata
nachylenia krawędzi bocznej do płaszczyzny podstawy oraz objętość ostrosłupa. Bardzo proszę o
pomoc.
3 maj 22:17
:O: majstruję...
3 maj 22:42
Tadeusz:
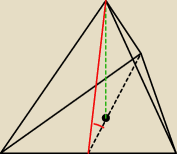
3 maj 22:53
duo: Wykombinuj coś. Plisss...
3 maj 22:54
:O:
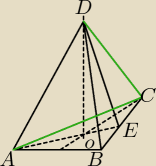
|AD|=2
√7
ΔOED − prostokątny
|∡OED|=60
0
|∡DOE|=90
0
|∡ODE|=30
0 ← trójkąt specjalny
|OE|=x, |DO|=x
√3, |DE|=2x
ΔAOD:
(2
√7)
2=(2x)
2+(x
√3)
2 ⇒ x=2
ΔABC − równoboczny ⇒ |AO|=2|OE|=2*2=4
|AE|−wysokość podstawy
h=6
6=U{a
√3{2} ⇒ a=4
√3
jeżeli się nie pieprznąłem w obliczeniach
3 maj 22:59
duo: Dzięki bardzo, ale nie bardzo rozumiem dlaczego taki tangens . krawędź boczna wynosi 2√7
3 maj 23:13
:O:
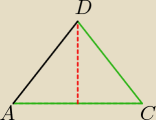
Narysuje trójkąt ACD
|AD|=2
√7
| | 4√3 | | 1 | |
czerwona wysokość dzieli podstawę |AC| na połowę = |
| * |
| = 2√3 |
| | 2 | | 2 | |
h było wcześniej policzone z "trójkąta specjalnego" = 4
3 maj 23:19
:O: masz jakieś odpowiedzi? sprawdź wynik bo nie jestem pewny
3 maj 23:20
duo: Już rozumiem. Jest dobrze nie zwróciłam uwagi, że chodzi o tg kąta. Jestem ogromnie wdzięczna.
3 maj 23:25
:O: PRONTO, MORDO!

3 maj 23:26

 |AD|=2√7
ΔOED − prostokątny
|∡OED|=600
|∡DOE|=900
|∡ODE|=300 ← trójkąt specjalny
|OE|=x, |DO|=x√3, |DE|=2x
ΔAOD:
(2√7)2=(2x)2+(x√3)2 ⇒ x=2
ΔABC − równoboczny ⇒ |AO|=2|OE|=2*2=4
|AE|−wysokość podstawy
h=6
6=U{a√3{2} ⇒ a=4√3
|AD|=2√7
ΔOED − prostokątny
|∡OED|=600
|∡DOE|=900
|∡ODE|=300 ← trójkąt specjalny
|OE|=x, |DO|=x√3, |DE|=2x
ΔAOD:
(2√7)2=(2x)2+(x√3)2 ⇒ x=2
ΔABC − równoboczny ⇒ |AO|=2|OE|=2*2=4
|AE|−wysokość podstawy
h=6
6=U{a√3{2} ⇒ a=4√3
 Narysuje trójkąt ACD
|AD|=2√7
Narysuje trójkąt ACD
|AD|=2√7
