dany jest trójkat abc, suma długości boku AB...
jola:
Zadanko z matury PWN którego nie kapuje pomimo że w odpowiedziach jest to rozpisane.
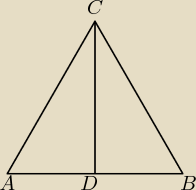
Dany jest trójkąt ABC, suma długości boku AB i wysokości opadającej na ten bok wynosi 20 cm.
Ile powinna wynosić dlugość boku AB i wysokości opadającej na ten bok, aby pole tego trójkąta
było
największe?
|AB|+ |CD|= 20
|AB|= a
|CD|= h
a+h=20 h=20−a
P=
12 a*h =
12 a* (20−a) = 10a−
12a
2 = a (10−
12a)
i co dalej ?
http://www.akademiapwn.pl/pl/aktualnosci/arkusze-maturalne-od-ampwn-matematyka.html
3 maj 15:53
patii: P=−12a2+10a
pole jest funkcja kwadratowa wspolczynnik przy najwyzszej potedze jest ujemny zatem parabola
bedzie skierowana ramionami w dół i wartosc najwieksza jest po prostu dla wieszcholka tej
paraboli
3 maj 16:08
PW: Mówiąc ściślej funkcja P osiąga największą wartość dla x, który jest pierwszą współrzędną
wierzchołka paraboli (druga współrzędna wierzchołka to wartość maksymalna, ale o to nie
pytali, więc nie liczymy i nie mówimy o tym w odpowiedzi).
3 maj 20:58
jola: dzięki wam

4 maj 09:37
 Zadanko z matury PWN którego nie kapuje pomimo że w odpowiedziach jest to rozpisane.
Dany jest trójkąt ABC, suma długości boku AB i wysokości opadającej na ten bok wynosi 20 cm.
Ile powinna wynosić dlugość boku AB i wysokości opadającej na ten bok, aby pole tego trójkąta
było
największe?
|AB|+ |CD|= 20
|AB|= a
|CD|= h
a+h=20 h=20−a
P= 12 a*h = 12 a* (20−a) = 10a− 12a2 = a (10− 12a)
i co dalej ?
http://www.akademiapwn.pl/pl/aktualnosci/arkusze-maturalne-od-ampwn-matematyka.html
Zadanko z matury PWN którego nie kapuje pomimo że w odpowiedziach jest to rozpisane.
Dany jest trójkąt ABC, suma długości boku AB i wysokości opadającej na ten bok wynosi 20 cm.
Ile powinna wynosić dlugość boku AB i wysokości opadającej na ten bok, aby pole tego trójkąta
było
największe?
|AB|+ |CD|= 20
|AB|= a
|CD|= h
a+h=20 h=20−a
P= 12 a*h = 12 a* (20−a) = 10a− 12a2 = a (10− 12a)
i co dalej ?
http://www.akademiapwn.pl/pl/aktualnosci/arkusze-maturalne-od-ampwn-matematyka.html
