geometria analityczna Anka:

	x1+x2+x3		y1+y2+y3
wykaż, że punkt P=(		;		) jest środkiem ciężkości trójkąta ABC,w
	3		3

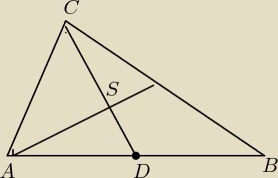którym A=(x1;y1), B=(x2;y2), C=(x3;y3)

Bogdan: podpowiedź: Punkt ciężkości trójkąta S, czyli punkt przecięcia środkowych trójkąta dzieli każdą środkową na dwa odcinki w stosunku 1 : 2.

bolek: jak to zrobic?

AS: Przyjmuję A(x1,y1) , B(x2,y2) , C(x3,y3) D(xD,yD) − środek odcinka AB xD = (x1 + x2)/2 , yD = (y1 + y2)/2 Korzystam z wzoru na podział odcinka w danym stosunku (u nas k = 2)

	x3 + k*xD		y3 + k*yD
xs =		ys =
	1 + k		1 + k

	x3 + 2*(x1 + x2)/2		x1 + x2 + x3
xs =		=
	1 + 2		3

Analogicznie postępujemy z ys