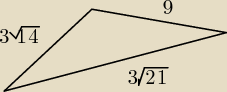
 Jak najprościej to pole policzyć ?
boki tego trójkąta to 9, 3√14 i 3√21 jak obliczyć pole mam
Jak najprościej to pole policzyć ?
boki tego trójkąta to 9, 3√14 i 3√21 jak obliczyć pole mam 
| 26 | 13 | |||
cosα = | = | |||
| 14√6 | 7√6 |
| 169 | 169 | 125 | ||||
sin2α = 1 − | = 1− | = | ||||
| 49*6 | 294 | 294 |
| √125 | 5√5 | |||
sinα = | = | |||
| √294 | 7√6 |
| 1 | 5√5 | |||
P = | *3√14*3√21* | = | ||
| 2 | 7√6 |
| 1 | 5√5 | ||
*9*√2*7*3*7* | = | ||
| 2 | 7√6 |
| 1 | 5√5 | ||
*9*7√6* | = | ||
| 2 | 7√6 |
| 45√5 | |
| 2 |
| 1 | ||
cosγ= | ||
| 3√14 |
| 1 | ||
sin2γ=1− | ||
| 9*14 |
| 1 | ||
sin2γ=1− | ||
| 126 |
| 125 | ||
sin2γ= | ||
| 126 |
| 5√5 | ||
sinγ= | ||
| 3√14 |
| 1 | 5√5 | |||
PΔ= | *3√14*9* | |||
| 2 | 3√14 |
| 45√5 | ||
PΔ= | ||
| 2 |
| 14*9+21*9−9*9 | 26*9 | 13 | ||||
cosα= | = | = | ⇒ | |||
| 2*3√14*3√21 | 2*9*7√6 | 7√6 |
| 132 | 132 | 6*72−132 | ||||
⇒ cos2α= | ⇒ sin2α=1−cos2α= 1− | = | , więc | |||
| 6*72 | 6*72 | 6*72 |
| √6*49−169 | ||
P=12*9*7√6* | = 4,5√125= 5*4,5√5=22,5√5 . ...  | |
| 7√6 |