Pomocy!!! asd: Wiadomo, że α jest kątem ostrym i tgα+ctgα=4. Oblicz √tg²α+ctg²α

Kejt: √tg²x+ctg²x−2tgxctgx+2tgxctgx=√(tgx+ctgx)²−2tgxctgx=... ctgx*tgx=1

Nienor: Jeżeli α jest ostry, to tgα+ctgα>0, więc można podnieść do kwadratu: (tgα+ctgα)²=16 Plus tgα*ctgα=1 (zastanów się dlaczego )

asd: Nie wiem nie ogarniam, jak do tego doszło O.o

Kejt: to sprytny trik którego fragmentu nie rozumiesz?

Dziabong: Przypomnij sobie jak można rozpisać tg i ctg.

Nienor:

	b
tgα=
	a

	a
ctgα=
	b

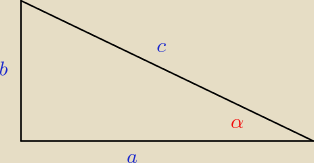
A teraz policz tgα*ctgα=...

asd: 2tgxctgx+2tgxctgx=√(tgx+ctgx)2−2tgxctgx=.. tego konkretnie skąd to się wzięło

Kejt: zauważ, że 2tgxctgx i −2tgxctgx się redukują, więc nie zmieniają naszego przykładu, zapisałam to tak tylko po to, by móc skorzystać ze wzoru skróconego mnożenia(żebyś to widział/a), a co za tym idzie własności podanej w zadaniu.

asd: Ok dzięki