Własności prawdopodobieństwa
Krzysiu: Zdarzenia losowe A, B są zawarte w Ω oraz P(A∩B`)=0.1 i P(A`∩B)=0.2 Wykaż, że P(A∩B)≤0.7
Proszę o sprawdzenie, czy to zadanie można rozwiązać w ten sposób:
Zdarzenia AnB i A'nB i AnB' są parami rozłączne
AnB ⊂(Ω − AnB' − A'nB), więc
P(AnB)≤ P(Ω)− P(AnB')− P(A'nB)= 1 − 0,1 − 0,2 = 0,7
P(AnB)≤ 0,7
to kończy dowód
2 maj 15:10
Krzysiu: podbijam
2 maj 16:35
Krzysiu: podbijam
2 maj 18:04
2 maj 18:09
Krzysiu: Dzięki, jednak bardziej zależy mi na sprawdzeniu tego, co napisałem. Jest to dla mnie bardziej
intuicyjne.
2 maj 18:18
Krzysiu: podbijam
2 maj 19:12
Use:
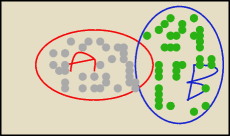
na szaro P(AnB") na zielono P(BnA")
widac wyraznie z rysunku że P(AnB")+P(BnA")+P(AnB)=P(AuB)
z koleji P(AuB)≤1
czyli ; 1≤P(AnB")+P(BnA")+P(AnB)
podstawiamy i mamy gotowe, dobrze jest rysowac sobie pomocniczo sytuacje ( bo to nic innego jak
rachunek zbiorow )
2 maj 19:25
