Dana jest f. f(x)= x^2 + 2|x|. Okresl lb. rozw. dla f(x)=m merbb: Nie wiem jak sie zabrac za ten |x|

Use: f(x)=x²+2x ,gdy x≥0 f(x)= x²−2x , gdy x<0 (powinno sie to piasac tak ze f(x)= robisz klamerke i piszesz dwa przypadki )

xyz: Rozpisz z definicji wartosci bezwzglednej x i pozniej narysuj wykres funkcji w 2 przedzialach

merbb: kapuje dzieki

merbb: nie wiem albo nie mysle albo nie mam pojecia ale czy moglby ktos mi zrobic rysunek bo nei jestem pewien jak to powinno wygladac

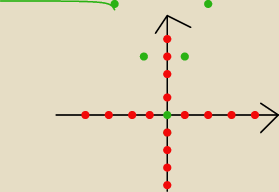
Use: normalnie jak nie wiesz jak narysowac to narysuje tabelke x i y i podstawiaj kilka liczb ( z tym ze jak podstawiasz liczbe to zwroc uwage z jakiego wzoru skorzystasz bo dla x<0 masz inny wzor niz dla x≥0) parabola bedzie z tego co widze ale narysuj sobie w zeszycie porzadnie oblicz kilka punktow i bedzie tak jak trzeba

Use: no i masz rusunek do dupy ,

merbb: ok ale mam x² + 2x x≥0 podstawiam 1 − wychodzi 3 podstawiam 2− wychodzi 8 x² −2x x<0 podstawiam −1− wychodzi 3 podstawiam −2 − wychodzi 8 to cos srednio parabole widze

xyz: Tabelka to chyba zly pomysl do tego... Masz 2 funkcje okreslone w 2 przedzialach, policz ich miejsca zerowe i wspolrzedne wierzcholkow to narysujesz

merbb: rozumiem ze takie cos x² + 2x −− zamienie na (x+1)² −2 z tgeo wynika z p= −1 i q=−2 i z tym 2 to samo ?

Use: a faktycznie kurde xyz ma racje masz dwie funkcje kwadratowe rysujesz po prostu te dwie parabole i zostawiasz czesc paraboli ( ktora zachodzi w dziedzine ) i dostaniesz cos w rodzaju polaczenia ramion dwoch parabol

merbb: tam powinno byc (x+1)² −1

Use: p=−b/2a czyli p =−2/2=−1 a q = f(p) czyli q= (−1)²+2*−1=1−2=−1

merbb: wiem wiem machnalem sie na obliczeniach ale jak z rysunkiem? mam sie trzymac tych x≥0 i x<0 ?

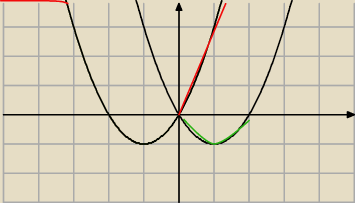
merbb: takie cos ?XD

merbb: cos tam sie nie zaznacza ale powinna lewa czesc lewej paraboli byc na czerwono

Use: no wlasnie teraz zaznaczasz ktora parabola jest dla x<0 i ktora jest dla 0≤x ( parabole ktora jest dla x<0 zaznaczasz na przedziale gdzie iksy sa mniejsze od zera a ta druga na przedziale gdzie isky sa wieksze badz rowne zero

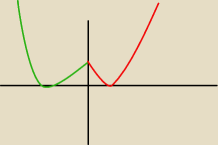
Use: prawdopodobnie wyjdzie cos takiego jak wyzej

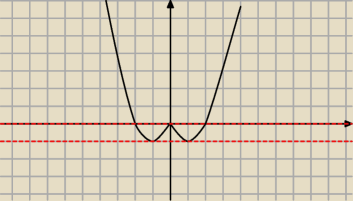
Kipic: 2 rozwiazania dla m=−1 i m∊(0;+∞) 3 rozwiazania dla m=0 4 rozwiazania dla m∊(−1;0)

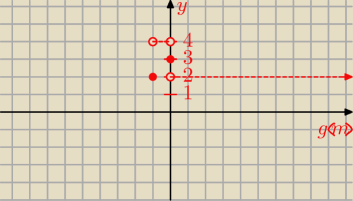
Kipic: a tu jakby jescze chcieli wykres g(m)=y