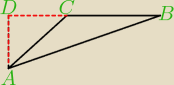
Obwód trójkąta, promień koła i sinus kąta wewnętrznego. falafel: W trójkącie ABC bok AB jest o 5 dłuższy od boku AC, zaś kąt ACB = 150. Wiedząc, że BC = 3√3, oblicz: obwód tr. ABC, promień koła opisanego na tym trójkącie, sinus kąta wewnętrznego przy wierzchołku A. Udało mi się stworzyć coś takiego. Jako, że kąt DCA ma 30 stopni, ADC 90, a DAC 60 to udało mi się wyliczyć taką zależność, że DC = x, AC = 2x i DA = x√3. Co prawda wyliczyłem obwód ze wzoru (x√3)² + (x+3√3)² = (2x+5)². Po całym szeregu obliczeń wyszło mi, że x=(10 + 3√3)/73, więc cały obwód (40 + 12√6)/73 + 5 + 3√3 Nie mam żadnej pewności czy jest to dobry wynik ani jak policzyć pozostałe dwa podpunkty.

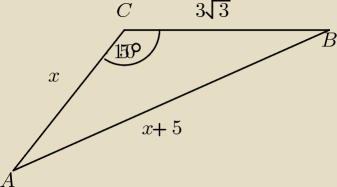xyz: Ja bym to zrobił z cosinusów: (x+5)² = x² +(3√3)² − 2*x3√3cos150