matura 2013
camel: Ciąg (a,b,c) jest ciągiem arytmetycznym. Suma jego wyrazów jest równa 18. Jeżeli pierwszą z
liczb zmniejszymy o 25% a trzecią o zwiększymy o 50%, to otrzymamy trzy kolejne wyrazy ciągu
geometrycznego. Wyznacz liczby a,b,c
Dany jest równoramienny trójkąt prostokątny, którego przeciwprostokątna ma długość 2. Bok AB
prostokąta ABCD zawiera się w przeciwprostokątnej tego trójkąta, zaś punkty C i D należą do
przeciwprostokątnych. Oblicz długości boków prostokąta ABCD wiedząc, że kwadrat długości jego
przeciwprostokątnej AC ma wartość najmniejszą z możliwych.
Bardzo proszę o pomoc
1 maj 19:32
camel: damy rade ?
1 maj 20:07
Mila:
a+b+c=18
a+a+r+a+2r=18
3a+3r=18
a+r=6⇔b=6, zapiszemy c. arytmetyczny w zależności od r
6−r,6,6+r
Zmieniamy odpowiednio wyrazy
| 3 | | 3 | |
| (6−r), 6 , |
| (6+r) − kolejne wyrazy c. geom.⇔ |
| 4 | | 2 | |
r=2 lub r=−2
C. Arytm. 4,6,8 lub
8,6,4
spr.
ciąg:3,6,12 jest geometryczny , q=2
ciąg: 6,6,6 ciąg geom. stały
1 maj 22:12
Mila:
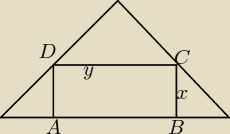
Popraw treść zadania .
Punkty Ci D należą....
Kwadrat.....
1 maj 22:19
camel: zaś punkty C i D należą do
przeciwprostokątnych. Oblicz długości boków prostokąta ABCD wiedząc, że kwadrat długości jego
przeciwprostokątnej AC ma wartość najmniejszą z możliwych.
2 maj 09:24
camel: ale czy te ciąg można traktować jaka kolejne wyr jak tam pisze że jest on tylko cięgiem
arytmetycznym ?
2 maj 09:25
Mila: Camel, w trójkącie prostokątnym masz jedną przeciwprostokątną i 2 przyprostokątne, w
prostokącie nie ma przeciwprostokątnej lecz jest przekątna.
Chodzi mi o to, abyś nie mylił pojęć. To ważne.
Po obiedzie pomogę, jeśli nikt nie napisze wcześniej.
2 maj 13:10
Mila:
2 maj 13:11
camel: sorry Mila już mi się miesza wszystko. Wybacz to takie drobne błędy słowne

2 maj 14:13
camel: Dany jest równoramienny trójkąt prostokątny, którego przeciwprostokątna ma długość 2. Bok AB
prostokąta ABCD zawiera się w przeciwprostokątnej tego trójkąta, zaś punkty C i D należą do
przyprostokątnych. Oblicz długości boków prostokąta ABCD wiedząc, że kwadrat długości jego
przekątnej AC ma wartość najmniejszą z możliwych.
Tak ma być

2 maj 14:26
Mila: Tak. Piszę.
2 maj 15:07
Mila:
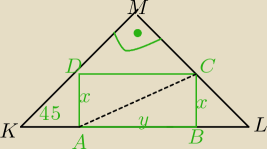
|KL|=2
|AC|
2=x
2+y
2
W ΔKAD:
2x=2−y
y=2−2x
|AC|
2=f(x)=x
2+(2−2x)
2
f(x)=x
2+4−8x+4x
2
f(x)=5x
2−8x+4 parabola skierowana ramionami do góry,
wartość najmniejsza w wierzchołku paraboli
odp.
2 maj 15:30
camel: całkiem sprytnie

Mila ale jeszcze takie pytanie do zadania pierwszego : potraktowałaś to jak
trzy kolejne wyr ciągu arytmetycznego. Skąd wiesz ze tak jest ?
2 maj 18:47
Mila: Tak pisze, że jest to ciąg arytmetyczny.
2 maj 19:00
camel: czyli spokojnie moge potraktować to jako kolejne wyr ciągu arytmetycznego ?
2 maj 19:14
 Popraw treść zadania .
Punkty Ci D należą....
Kwadrat.....
Popraw treść zadania .
Punkty Ci D należą....
Kwadrat.....


 |KL|=2
|AC|2=x2+y2
W ΔKAD:
|KL|=2
|AC|2=x2+y2
W ΔKAD:
 Mila ale jeszcze takie pytanie do zadania pierwszego : potraktowałaś to jak
trzy kolejne wyr ciągu arytmetycznego. Skąd wiesz ze tak jest ?
Mila ale jeszcze takie pytanie do zadania pierwszego : potraktowałaś to jak
trzy kolejne wyr ciągu arytmetycznego. Skąd wiesz ze tak jest ?