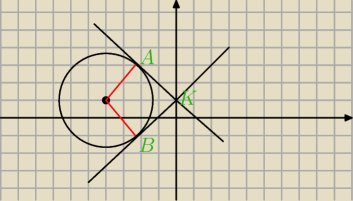
Dany jest okrag o rownaniu x^2 +8x+ y^2 -2y +9=0. Znajdz rownanie stycznej przec merbb: Ustailem ze okrag ma rownanie (x+4)² +(y−1)²=8 i narysowalem go. Utknalem na tym ze nie wiem co zrobic z tymi punktami A i B

merbb: Dany jest okrag o rownaniu x² +8x+ y² −2y +9=0. Znajdz rownanie stycznej przechodzaje przez punkt K (0,1)

Dominik: za malo danych.

merbb: dopisalem, wiecej nic nie ma, dlateog nie mam pojecia co zrobic

xyz: Prosta przechodząca przez punkt K: y=ax + 1 Masz srodek, masz promien. liczysz odleglosc srodka od prostej i wychodzi wspolczynnik a

Dominik: okej, widze ze dopisales. rownanie stycznej: y = ax + b wiadomo, ze przechodzi przez punkt (0, 1), zatem b = 1 stad rownanie ma postac y = ax + 1 wystarczy rozwiazac uklad rownan

⎧	(x + 4)2 + (y − 1)2 = 8
⎨
⎩	y = ax + 1

i do rownania kwadratowego ze zmienna x dac warunek Δ = 0. lub przeksztalcic rownanie prostej do postaci ogolnej ⇒ ax − y + 1 = 0 i podstawic do wzoru na odleglosc punktu od prostej, wiedzac ze odleglosc srodka okregu od stycznej jest rowna promieniowi.

|−4a|
	= 2√2
√a2 + 1

merbb: a w tym rownaniu dominik to jaki punkt mam dac ten x0 i y0 ?

Dominik: gdzie chcesz dawac x0 i y0? wstaw y do rownania okregu, podnies nawiasy do kwadratu i dostaniesz rownanie kwadratowe z parametrem. wystarczy wyliczyc wartosc parametru a dla ktorego Δ = 0.

Dominik: druga metoda prawde mowiac jest szybsza i latwiejsza.

merbb: rozwiazalem ten uklad rownan i rozumiem ze powinno wyjsc a=1 v a= −1 i y= −x +1 i y=x +1 ?

merbb: mi chodzilo o ta 2 metode, w tym −4a , ktore mam wstawiac do rowniania Ax0 + By0 itd..

merbb: ok mam jeszcze 2 zadanie gdzie tresc brzmi : oblicz wartosc m i n dla ktorych wielomian w(x)= x⁴ + x³ +mx² −4x + n jest podzielny przez p(x)= x²+x+1. Podzielilem jeden przez drugi i wyszlo mi u gory x² +(m−1) i reszta (−m−3)x + n −m +1. Wiem ze trzeba ja przyrownac do reszty jesli jeden wielomian dzieli drugi ale ten x mi strasznie przeszkadza i nie wiem co dalej zrobic

Dominik: Ax + By + C = 0 dla naszej prostej A = a, B = −1, C = 1

	Ax0 + Bx0 + C
d =
	√A2 + B2

x₀, y₀ to wspolrzedne srodka okregu, czyli x 0 = −4 y₀ = 1 ponadto d = r = 2√2 wyniku nie znam; zakladam ze w gimnazjum naliczyli ciebie liczyc. jak chcesz sie upewnic to zapisz obliczenia.

Dominik: zakladam, ze dzielenie jest wykonane dobrze. mamy reszte w postaci ax + b. widac, ze zeruje sie dla kazdego x, gdy a = 0 i b = 0. zatem − m − 3 = 0 ∧ n − m + 1 = 0

Mila: Jeśli dzielisz przez wielomian II stopnia to reszta może być wielomianem stopnia I, reszta ma postać: R(x)=ax+b Dobrze podzieliłeś. m=−3 i n=−4 W(x)=(x²−4)*(x²+x+1)