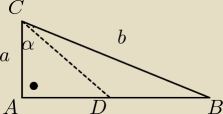
W trójkącie prostokątnym ABC, przez wierzchołek C kąta prostego poprowadzono... Karygodny: W trójkącie prostokątnym ABC, przez wierzchołek C kąta prostego poprowadzono prostą, która przecięła bok AB w punkcie D. Wiedząc, że |AC|=a, |BC|=b oraz |<ACD|=30 stopni, oblicz: a) |CD| b)|AD| : |DB|

Karygodny: Proszę o pomoc!

bżdonc:

	a√3
α=30 ⇒ |∡ADC|=60 ⇒ |CD|=2a ⇒ |AD|=
	3

|∡ADC|=60 ⇒ |∡CDB|=120 cos120=cos(90+30)=−sin30 i teraz z tw. cosinusów możesz policzyć |DB|

Karygodny: A to |CD| nie ma wychodzić czasem z kąta prostego?

bżdonc: Ah, no tak, sorrki

Karygodny: Pomoże ktoś ?

Karygodny: ?

Karygodny: ref

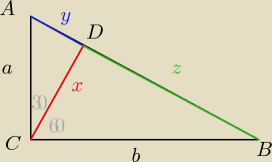
Saizou : P_ABC=P_ACD+P_BCD

a*b		1		1
	=		*a*x*sin30+		*b*x*sin60
2		2		2

ab=ax*sin30+bx*sin60

	1		√3
ab=ax*		+bx*
	2		2

2ab=ax+bx*√3 2ab=x(a+b√3)

	2ab
x=
	a+b√3

Eta:

kakakakakakkakaka: a przykład b?