tryg xyz: Dla jakich wartości parametru m rownanie ma rozwiązanie: sin²x + sinx + m = 0 sinx=t , t∊<−1;1> t² + t + m = 0 Δ≥0 I tutaj jakie maja byc warunki? f(−1)>0 f(1)>0 −1<x_w<1 ?

Saizou : −sin²x−sinx=m

	1
zauważ że dziedziną funkcji f(x)=−sin2x−sinx jest przedział <−2:		>, zatem
	4

	1
−2<m<
	4

xyz: Tez podejrzewalem ze w ten sposob sie da, ale te warunki tez sa dobre?

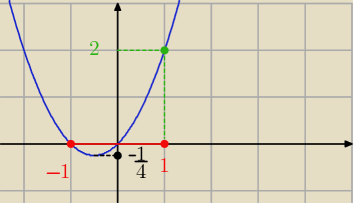
Nienor: Równanie t²+t+m=0 może mieć tylko jedno rozwiązanie z przedziału [−1,1] i warunek zadania będzie spełniony. Należy rozważyć takie równanie t²+t i zapytać jakie musi być m, aby dla t∊[−1,1] istniało choć jedno rozwiązanie. Najlepiej to narysować.

	−1
Wynika z tego, że m∊[		,2]
	4

Saizou : poprawka nie dziedziną tylko zbiorem wartości

bżdonc: @Saizou: jak to określiłeś?

xyz:

	1
Saizou ale jak ci wyszla dziedzina ;		> ?
	4

Nienor: Saizou dlaczego zamieniłeś znaki

	−1
xyz nie wystarczą twoje warunki, one wyznaczą ci m∊[		,0].
	4

xyz: To jakie warunki tutaj muszą być?

Nienor: Masz rozwiązanie o 18:55

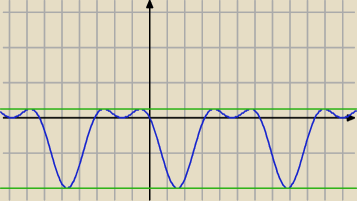
Saizou : zbadałem jaki przebieg ma funkcja. W tym celu powstawiałem sobie do wzoru

	π		π		π		π
x∊{0:		:		:		:		} oczywiście dla ujemnych też i uwzględniając powtarzalność
	6		4		3		2

warto nawet narysować sobie przybliżony wykres

Nienor: Mi chodzi o to, że badana funkcja to f(x)=sin²x+sinx+m, a nie f(x)=−sin²x−sinx+m

xyz: sin²x + sinx przeniósł na prawą, żeby po elwej zostało samo m

Saizou : ale ja badam funkcję f(x)=−sin²x−sinx

xyz:

	1
I w zasadzie to tez myslalem ze tak bedzie... tylko z tego psosobu wychodzi m ∊ [−2;		]
	4

xyz: Wie ktos jak to zrobic z zalozeniami?

xyz: @Nienor, ale tam przy twoim rozwiązaniu to nie powinny być przeciwne znaki przy określaniu m? Bo po przekształceniu równania wygląda ono tak: sin²x + sinx = −m