oblicz pole powierzchni stożka mila21121973: 1. Oblicz pole powierzchni bocznej stożka wiedząc, że, przekrój osiowy stożka jest trójkątem równobocznym o boku l=2 2. Promień okręgu opisanego na ostrosłupie prawidłowym trójkątnym jest równy R=4 cm. , zaś krawędź boczna ostrosłupa ma długość l=5cm. Oblicz objętość tego ostrosłupa. Dokończ rysunek i wprowadź oznaczenia Będę wdzięczna za pomoc.

mila21121973: Ten rysunek jest do zadania 2

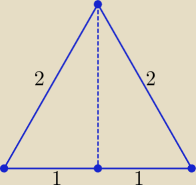Bogdan: 1. Zastosuj wzór na pole powierzchni bocznej stożka.

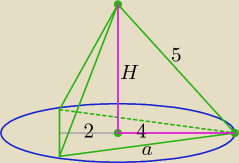Bogdan: 2. Treść zadania jest nieprawidłowa. Powinno być: "Promień okręgu opisanego na podstawie ostrosłupa...".

	1
Pole powierzchni trójkąta równobocznego o boku a: P =		a2√3.
	4

	1		1
Objętość V =		*		a2√3 * H.
	3		4

	1		1
R =		a√3 ⇒ 4 =		a√3 / *√3 ⇒ a = 4√3
	3		3

Wysokość ostrosłupa H oblicz korzystając z twierdzenia Pitagorasa.

mila21121973: Dzieki serdeczne za pomoc.Widocznie jest błąd w druku.Pozdrawiam