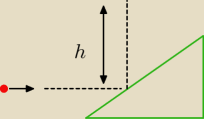
Matura Technik: Matura ale z fizyki Sprawdzi ktoś W równię pochyłą o masie 0,28 kg uderza poziomo kula o masie 0,12 kg i odbija się do góry. Na jaką wysokość wzniesie się kulka po uderzeniu,jeśli równia odskakuje z prędkością 1,25 m/s ? Tarcie można zaniedbać, a zderzenie jest sprężyste. a więc tak m₁=0,28kg m₂=0,12kg v=1,25m/s g=9,81

	m1(m1−m2)v2
h=
	2(m2)2g

	0,28(0,28−0,12)*(1,25)2
h=		=25cm
	2*(0,12)2*9,81

ok

Kipic: @Technik ale zadanie dla mnie przepasc

Technik: @Kipic zadanie nie jest trudne Ty za to wymiatasz z matmy a i jeszcze jedno zapomniałem Ci napisać poucz się dobrze konstrukcji w zwierciadle i soczewkach bo to często jest i trzeba bardzo dokładnie rysować a sprawdzający się czepiają

Licealista_Theosh: Techniku nie wiem czy dobrze, ale ja to zrobiłem tak: E_k=E_p

1		m
	(0,12kg) * (1,25		)2 = 0,28 kg *9,81 * h
2		s

	m
0.09375J = 2,748 kg*		*h
	s2

h=0,03m = 3 cm.

Licealista_Theosh: Ups chodziło mi o zasadę zachowania pędu a nie energii. Nie sprawdzaj jest źle.

Kipic: @Technik soczewki, zwierciadla, rzut pionowy ukosny poziomy , liczenie oporow, zadania zwiazane z predkosciami , prawie zawsze cos z tego jest hehe

Technik: @Kipic wyślę Ci na pocztę zadania z tego co napisałeś z rozwiązaniami to sobie będziesz sprawdzał @Licealista Theosh

Kipic: @Technik dzięki

Licealista_Theosh: No co...

Licealista_Theosh: A zjarzyłem. Źle przekształciłem wzór, ale chodziło mi o to Takie zadania są na rozszerzeniu?

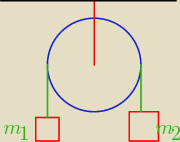
Technik: To jeszcze jedno (już ostatnie) trzeba tylko wyznaczyć wzóry Oblicz przyspieszenie układu i siły naciągów nici układu przedstawionego na rysunku. Moment bezwładności bloku I, a jego promień R (m₁>m₂). najpierw przyspieszenie a

	(m2−m1)*R2
a=		*g
	I+(m1+m2)*R2

	(m2−m1)*R2
FN1=m1g(1+		)
	I+(m1+m2)R2

	(m2−m1)R2
FN2=m2g(1−		)
	I+(m1+m2)R2

Technik: @Licealista Theosh tak są na rozszerzeniu , to zadanie jest z próbnej matury ułożonej przez moją nauczycielkę od fizyki

Technik: @Kipic fajna stronka z fizyką od podstaw http://fizyka.org/

Kipic: @Technik tak sobie przegladalem i 1 co sukalem to opis rozdzialu Praca Moc Energia Te energie : potencjalna i kinetyczna poniewaz mnie rozbrajaja Całkiem dobra strona

Technik: a w czym masz problem z tą energią kinetyczną i potencjalna może dam Ci jakiegoś linka

Kipic: no nie ogarniam kiedy cialo ma potencjalna a kiedy kinetyczna np/; pocisk sobie leci pionowo z jakas szybkoscia V uderza w worek i mam obliczyc zaleznosci medzy energiami w czasie uderzenia i z jaka energia wyleci on z worka przed uderzeniem v₀ =120m/s po przebiciu V_k=72m/s d−srednica worka 0,4m wogule to zadanie rozwala system nie moge ogarnac

Technik: Gdy ciało spada swobodnie energia potencjalna zamienia się w energię kinetyczną co też wynika ze wzorów (prędkość rośnie więc energia kinetyczna rośnie, natomiast wysokość maleje więc energia potencjalna maleleje). Czyli ile ubędzie energii potencjalnej tyle przybędzie energii kinetycznej.

Technik: ale ten pocisk wystrzelona z jaką prędkością napisz pełną treść i wyśli na email to odpowiem bo teraz idę na konsultację z matematyki więc nie pomogę w tej chwili

Kipic: w teorii oczywiste ale ak zaczynam robic zadania to w praktyce nie rozumiem musze jescze sporo zadan zrobic

Kipic: @Technik to zadanie nam dal kolo z fizy jak znajde ta kartke to napisze

Nienor: Zadanie 1. Kipic zadania z fizyki to sztuka wyciągania co się da z treści. Pisze, że zderzenie jest sprężyste Więc zachowana jest zasada zachowania energi:

m2vp2		m1v2
	=m2gh+		, gdzie vp jest prędkością kulki przed zderzeniem.
2		2

W tym równaniu masz dwie niewiadome h i v_p, szukasz więc jeszcze jednego równania: zasada zachowania pędu. Pęd kuleczki przed zderzeniem (p₁=m₂v_p, poziome) nie może zniknąć, ale jest w całości przekazany równi pochyłej, więc:

	m1v
m2vp=m1v ⇒ vp=		podstawiasz do pierwszego równania i gotowe
	m2

Technik: @Nienor dobrze są te zadania

Nienor: Z bloczkiem, po prostu rozwiązać trzeba układ:

⎧	Iε=(FN2−FN1)R
⎜	m1a=m1g−FN1
⎨	m2a=FN2−m2g
⎩	a=εR

Nie chce mi się go przekształcać. Co do zadania, które rozwala system: E_k1=E_k2+E_p+Q

	mv2o
Ek1=		− energia pocisku przed zderzeniam
	2

	mv12
Ek2=		− energia kinetyczna po przebiciu
	2

E_p=mdg − energia jaka wynika ze zwiększenia wysokości pocisku Q − energia tracona na ciepło w wyniku przebijania worku(czasami w zad. trzeba ją pominąć

Technik: @Nienor właśnie rozwiązałem ten układ i wyszło takie coś

Nienor: No to jest dobrze

Technik: mam jeszcze dwa masz chwilę żeby sprawdzić

Nienor: Tak, ale pisz też te równania początkowe, żebym później nie musiała sie zastanawiać, hmm... a to skąd

Technik: ok

Technik: Po równi pochyłej nachylonej do poziomu pod kątem α=45^o zsuwa się bez tarcia z wysokości h=1 cm małe ciało. Szybkość początkowa wynosi zero, a ciało można uważać za punkt materialny o masie m=1 g i ładunku q=1mC. W punkcie A znajduję się drugi ładunek punktowy Q=5mC. Obliczyć szybkośc ciała, gdy osiaga punkt C rozwiązanie w następnym poście

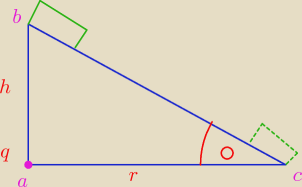
Technik: tam gdzie to czerwone kółeczko to kąt α a tam gdzie jest q powinno być duże Q punkt B− energia potencjalna grawitacji E_p1=mgh

	Qq
energia kinetyczna oddziaływania elekrost. Ep2=k
	h

energia kinetyczna E_k1=0

	mv2
punkt C Ek2=
	2

	Qq
energia potencjalna oddziaływania elektrosta Ep3=k
	r

energia potencjalna Ep₄=0 zasada zachowania energii E_p1+E_p2+E_k1=E_p3+E_p4+E_k2

	Qq		Qq		mv2
mgh+k		+0=k		+0+
	h		r		2

	2mgh		2kQq		2kQq
v2=		+		−
	m		mh		m*r

ciąg dalszy w następnym poście bo nie mogę już dodać rysunku

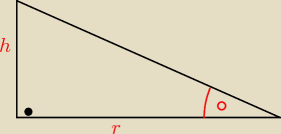
Technik: tam gdzie kółeczko to jest α

	h
tgα=
	r

	h
r=
	tgα

podstawiam z r do tamtego wzoru który wcześniej wyznaczyłem

	2kQq		2kQqtgα
v2=2gh+		−
	mh		m*h

	2kQq(1−tgα)
v=√ 2gh+		tutaj wszystko jest pod pierwiastkiem
	m*h

v=√0,2

	m
v≈0,45
	s

Nienor: Już po tamtym poście było widać, że dobrze

Technik: To dobrze bo zadania za 5 punktów

Technik: A mam jeszcze takie pytanie jaki jest wzór na pracę w przemianie adiabatycznej bo chyba na poziomie lo nie ma wzoru

Technik:

Nienor: Nie ma, bo to całka z pdV, po objętości, przy zależności pV^ϰ=const.

Technik: W cylindrze pod tłokiem jest 1 kilomol gazu dwuatomowego o temperaturze 27 stopni Celsjusza. Początkowo ga rozszerzał się adiabatycznie, aż objętość wzrosła 5−krotnie, a następnie sprężany izotermicznie do obj. początkowej. Obliczyć wykonaną pracę. zadanie znalazłem na internecie http://fizyczny.net/printview.php?t=32708&start=0&sid=864add4fe767783d4c989031959101af paskudny wzór to chyba nie jest na poziomie matury już

Nienor:

	pV0ϰ
W=∫[V0,5V0]		dV=pV0∫[V0,5V0]V−ϰdV=
	Vϰ

	−1		−1		−1
pV0[		V−ϰ+1]5V0V0=pV0(		*5V0−ϰ+1−		V0−ϰ+1)=...
	ϰ−1		ϰ−1		ϰ−1

	7
ϰ dla gazów dwuatomowych zwykle wynosi		.
	5

Technik: @Nienor ale to już chyba poziom expert całek nie ma w programie nauczania więc raczej nie spotkam tego na maturze ale dobrze wiedzieć jak się to liczy

Nienor: Bardzo prosta ta całka, nie taki znowu poziom ekspert Ale na maturze na pewno tego nie będzie Jakby podali molową pojemność cieplną, to mógłbyś skorzystać z: ΔU=Q+W, ale dla adiabaty Q=0 więc ΔU=W a ΔU=nC_VΔT

Technik: ale właśnie nie ma nic o molach niestety Mam nadzieje, że na tej maturze będzie bardzo mało zadań do wytłumaczenia jak coś tam działa i większości będą zadania obliczeniowe

Nienor: No u nas to więcej było takiej dziwnej teorii, ale pewnie wiesz. Więc może wy traficie na pożądne zadania

Technik: taką mam nadzieję przydałoby się napisać w granicach 80−90% było by super wtedy