stereometria, geometria
mimi:
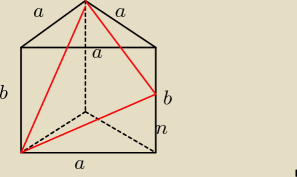
Suma długości wszystkich krawędzi graniastosłupa prawidłowego trójkątnego jest równa 60.
Wysokość jest o 2 większa od długości boku podstawy. Przez przekątną ściany bocznej i środek
krawędzi bocznej, niezawierającej się w tej ścianie, poprowadzono płaszczyznę. Oblicz pole
otrzymanego w ten sposób przekroju.
Proszę o pomoc z tym zadaniem, jak do tej pory obliczyłam wszystkie długości krawędzi tego
przekroju ale mam problem z obliczeniem pola. Obliczyłam, że krawędzie mają długość ; 5
√2,
5
√2 i 5
√5 . Zastanawiam się czy ten przekrój może być prostokątny?
30 kwi 22:59
m: jest tu ktoś...?
30 kwi 23:24
Mila:
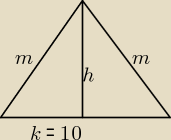
Rysunek przekroju:
6a+3b=60
6a+3*(a+2)=60
a=6
b=8
k
2=8
2+6
2=100
k=10
m
2=6
2+4
2
m
2=36+16
m=
√52
m=2
√13
Przekrój jest Δrównoramiennym o bokach:10,2
√13,2
√13
h
2+5
2=
√522
h
2=52−25
h=
√27
h=3
√3
dokończ
30 kwi 23:48
m: wielkie dzięki! wiem jaki głupi błąd zrobiłam... na samym początku zamiast b=a+2 ja napisałam
że b=2a ... −,− ... więc pole przekroju PΔ= 12 ah , stąd PΔ= 10*3√3=30√3
1 maj 00:03
 Suma długości wszystkich krawędzi graniastosłupa prawidłowego trójkątnego jest równa 60.
Wysokość jest o 2 większa od długości boku podstawy. Przez przekątną ściany bocznej i środek
krawędzi bocznej, niezawierającej się w tej ścianie, poprowadzono płaszczyznę. Oblicz pole
otrzymanego w ten sposób przekroju.
Proszę o pomoc z tym zadaniem, jak do tej pory obliczyłam wszystkie długości krawędzi tego
przekroju ale mam problem z obliczeniem pola. Obliczyłam, że krawędzie mają długość ; 5√2,
5√2 i 5√5 . Zastanawiam się czy ten przekrój może być prostokątny?
Suma długości wszystkich krawędzi graniastosłupa prawidłowego trójkątnego jest równa 60.
Wysokość jest o 2 większa od długości boku podstawy. Przez przekątną ściany bocznej i środek
krawędzi bocznej, niezawierającej się w tej ścianie, poprowadzono płaszczyznę. Oblicz pole
otrzymanego w ten sposób przekroju.
Proszę o pomoc z tym zadaniem, jak do tej pory obliczyłam wszystkie długości krawędzi tego
przekroju ale mam problem z obliczeniem pola. Obliczyłam, że krawędzie mają długość ; 5√2,
5√2 i 5√5 . Zastanawiam się czy ten przekrój może być prostokątny?
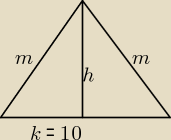 Rysunek przekroju:
6a+3b=60
6a+3*(a+2)=60
a=6
b=8
k2=82+62=100
k=10
m2=62+42
m2=36+16
m=√52
m=2√13
Przekrój jest Δrównoramiennym o bokach:10,2√13,2√13
h2+52=√522
h2=52−25
h=√27
h=3√3
dokończ
Rysunek przekroju:
6a+3b=60
6a+3*(a+2)=60
a=6
b=8
k2=82+62=100
k=10
m2=62+42
m2=36+16
m=√52
m=2√13
Przekrój jest Δrównoramiennym o bokach:10,2√13,2√13
h2+52=√522
h2=52−25
h=√27
h=3√3
dokończ