wartośc dla którego pole jest największe mmm: W kwadracie ABCD o boku długości 1 na boku AB wybrano punkt L. Na bokach BC i AD wybrano odpowiednio punkty M i K tak, że kąt KLM = 120 stopni , a dwusieczna tego kąta jest równoległa do boku BC. Oblicz długości odcinków LK i LM, dla których pole trójkąta KLM jest największe.

mmm:

mmm: ..

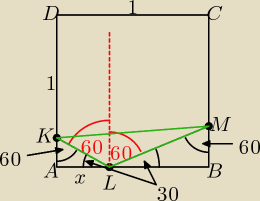
pomoc: niech IALI = x, wtedy ILBI = 1 − x i x∊(0;1). Z własn. trójkąta o kątach 30, 60 ,90 mamy:

	2√3x		2(1−x)√3
IKLI =		i ILMI =		.
	3		3

	1
Liczymy pole ΔKLM: P =		*IKLI*ILMI*sin120
	2

	1		2√3x		2(1−x)√3		√3		√3
P =		*		*		*		, bo sin120 = cos30 =
	2		3		3		2		2

	√3
po uproszczeniu: P =		*x*(1−x) i to pole ma być największe dla pewnego x∊(0;1).
	3

Tworzymy zatem funkcję P(x) i obliczamy argument x∊(0;1), dla którego ta funkcja osiąga wartość największą.

	√3		√3
A jest to funkcja kwadratowa P(x) = −		*x2 +		*x i x∊(0;1).
	3		3

Ta funkcja osiąga wart. największą wynoszącą y_W dla x_W.

	b
Czyli liczymy xW = −
	2a

	1
xW =		i xW∊(0;1).
	2

	1
Teraz wystarczy obliczyć KL oraz ML podstawiając x =		.
	2

	√3
Odp. IKLI = IMLI =
	3

beka: ∑∑∑∑∑∑∑∑

pigor: ..., W kwadracie ABCD o boku długości 1 na boku AB wybrano punkt L. Na bokach BC i AD wybrano odpowiednio punkty M i K tak, że kąt KLM=120^o, a dwusieczna tego kąta jest równoległa do boku BC. Oblicz długości odcinków LK i LM, dla których pole trójkąta KLM jest największe. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− a ja ... w swojej szufladzie widzę to tak: niech |LK|=x=?, |LM|=y=?, to P_KLM=¹₂xysin120^o=¹₂xysin60^o=¹₄√3xy=P_max, dla x,y= ? i własności trójkąta ekierki ¹₂x√3+¹₂y√3=1 ⇔ ⇔ √3(x+y}=2 /*√3 ⇔ 3(x+y)=2√3 ⇔ (*) x+y=²₃√3, stąd i z nierówności miedzy średnimi g≤a: P_KLM=¹₄√3xy ≤ ¹₄√3*¹₄(x+y)² = ¹₁₆√3*(²₃√3)²= ¹₁₆√3*⁴₃= ¹₁₂√3, przy czym równość, a tym samym P_max osiąga to pole ⇔ ⇔ x=y, czyli z (*) 2x= ²₃√3 ⇔ x= ¹₃√3=|LK|=|LM|.