zbiór
Saizou : ostatnio dopadłem w ręce zbiór z 1986r. pn.
Matematyka
zadania maturalne i egzaminacyjne
część I
autorstwa: T. Korczyc, j. Nowakowski
i mam pytanie miał ktoś do czynienia z tą książką ?
30 kwi 21:53
Kipic: Obstawiam ze zadania w tej ksiazce sa trudniejsze niz te co teraz sa

30 kwi 21:55
Saizou : chcesz jakieś zadanko z tego zbioru?
30 kwi 21:56
Nienor: Ja chcę, ja chcę

Może akurat będę wiedziała

30 kwi 21:57
Kipic: Zapodaj ciekawe czy tkne wogule hehe

tylko nie ciagi ani zbiory bo w tamtych ksiazkach to
chyab kosmos

30 kwi 21:57
Dominik: zarzuc jakas ciekawa geometrie plaska

30 kwi 21:57
Saizou : Rozważmy zbiór wszystkich prostokątów tak wpisanych w dany trójkąt ostrokątny ABC, że jeden z
boków każdego z nich jest zawarty w podstawie AB tego prostokąta. Oblicz długości boków tego
prostokąta, który ma największe pole, jeśli AB=a, CD=h gdzie CD jest wysokością trójkąta ABC
30 kwi 22:06
Dominik: takie same zadanko bylo w kielbasie.

zaraz policze
30 kwi 22:16
30 kwi 22:22
Saizou : zgadza się

30 kwi 22:24
xyz: To teraz napisz rozwiazanie
30 kwi 22:25
Nienor: A masz może jakieś zgrabne

Bo moje to duuużo proporcji, głównie Tales i ciężko to przenieść
na forum, więc jakbyś miał jakiś elegancki pomysł, to chętniebym zobaczyła

30 kwi 22:27
Kipic: No Talesem to troche lipa jest jakis inny sposob

30 kwi 22:30
Dominik:
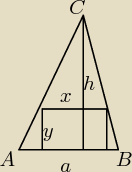
P = xy
y∊(0, h)
| | a(h − y) | | a | |
P(y) = y( |
| ) = |
| * y(h − y) |
| | h | | h | |
30 kwi 22:33
Nienor: Moje nie jest w połowie tak zgrabne. Brawo

30 kwi 22:35
Dominik: Saizou, dawaj wiecej

30 kwi 22:40
Kipic: @Dominik

świetnie rozwiązane zadanie

30 kwi 22:41
Saizou :
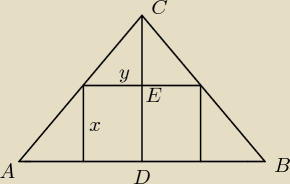
| | h−x | | ahx−ax2 | | a | |
Pprostokąta=xy=x*( |
| *a)= |
| = |
| (hx−x2) |
| | h | | h | | h | |
jest to funkcja kwadratowa skierowana ramionami w dół zatem maksymalną wartość przyjmuje dla
30 kwi 22:42
Saizou : Udowodnij, że dla każdej liczby naturalne n prawdziwa jest równość
| | n | |
12+32+.....+(2n−1)2= |
| (4n2−1) |
| | 3 | |
30 kwi 22:44
Dominik: da rade nieindukcyjnie? bo mialem z niej tylko pare lekcji w 2 klasie.

w kazdym razie −
musze sie zastanowic chwile.
30 kwi 22:46
Nienor: Z indukcji
Warunek pierwszy jest w oczywisty sposób zawsze spełniony.
2
o
| | k | |
Z: n=k i 12+32+...+(2k−1)2= |
| (4k2−1)
|
| | 3 | |
| | k+1 | |
T: n=k+1 i 12+...+(2k−1)2+(2k+1)2= |
| (4k2+8k+3)
|
| | 3 | |
Jeżeli do lewej i prawej strony założenia dodaliśmy tę samą liczbę, na mocy indukcji
matematycznej można stwierdzić, że teza jest prawdziwa. Wystarczy teraz wykazać, że:
T
L−Z
L=T
P−Z
P
T
L−Z
L=(2k+1)
2
| | (k+1)(4k2+8k+3)−k(4k2−1) | |
TP−ZP= |
| =
|
| | 3 | |
| 4k3+8k2+3k+4k2+8k+3−4k3+k | | 12k2+12k+3 | |
| = |
| =
|
| 3 | | 3 | |
4k
2+4k+1=(2k+1)
2
30 kwi 22:55
Dominik: no coz − indukcji obecnie w programie nie ma; ja jej odrobine liznalem, ale tak to z niej nie
korzystam i de facto poslugiwac sie nia nie potrafie. dopiero na studiach pojawia sie dowody
wymagajace indukcji.

30 kwi 22:58
Saizou : no to ostatnie zadanko na dziś, taki przyjemniejsze
Dane jest równanie
Dla jakich m jeden pierwiastek tego samego równania jest równy sinusowi, a drugi cosinusowi
tego samego kąta ostrego?
30 kwi 23:02
Saizou : | | 2 | |
odpowiedź to m= |
| , a ja lecę bo muszę wreszcie odespać nieprzespane noce, dobranoc |
| | 5 | |
30 kwi 23:05
Nienor: Jeżeli x1=sinα, a x2=cosα, to z faktu, że sin2α+cos2α=1, wynika, że x12+x22=1.
Oraz Δ≥0.
30 kwi 23:05
Trivial:
A jeśli chodzi o zadanie z sumą − wystarczy ją policzyć i po bólu!
S
n = 1
2+3
2 + ... + (2n−1)
2 = ∑
k=1..n (2k−1)
2 = [ ∑ (2x−1)
2 δx ]
1n+1
| | 4 | |
∑ (2x−1)2 δx = ∑ (4x2 − 4x + 1) δx = ∑ (4x(x−1) + 1) δx = |
| x(x−1)(x−2) + x + C. |
| | 3 | |
| | 4 | | 4 | | n | |
Sn = [ |
| x(x−1)(x−2) + x ]1n+1 = |
| (n−1)n(n+1) + n+1 − 1 = |
| (4n2−1) |
| | 3 | | 3 | | 3 | |
30 kwi 23:10
Dominik: Δ > 0
5m
2 + 10m − 24m + 5 ≥ 0
5m
2 − 14m + 5 ≥ 0
Δ
m = 96
√Δm = 4
√6
| | 14 + 4√6 | | 7 + 2√6 | |
m1 = |
| = |
| |
| | 10 | | 5 | |
| | 7 − 2√6 | | 7 + 2√6 | |
m∊(−∞, |
| >∪< |
| , ∞) |
| | 5 | | 5 | |
x
12 + x
22 = 1
(x
1 + x
2)
2 − 2x
1x2 = 1
5m
2 + 10m − 12m = 0
5m
2 − 2m = 0
m(5m − 2) = 0
| | 2 | |
m = |
| ∨ m = 0 − sprzecznosc |
| | 5 | |
30 kwi 23:11
Dominik: Trivial − rzeczywiscie po bolu, dla maturzysty.

30 kwi 23:12
Trivial: Sposób w sam raz dla maturzysty.

30 kwi 23:15
zombi: Trivial to było przez części tak? Można też tak na luzaku
| | n(n+1)(2n+1) | | n(n+1) | |
∑ (2k−1)2 = ∑4k2−4k+1 = 4∑k2 − 4∑k+n = 4( |
| − |
| )+ n = |
| | 6 | | 2 | |
| | 4n(n2−1)+3n | | n(4n2−1) | |
= |
| = |
| kuniec. |
| | 3 | | 3 | |
30 kwi 23:26
Trivial: Nie było przez części, tylko przez sprowadzenie do potęg dolnych
∑xnδx = (1/n+1)*xn+1
30 kwi 23:30
zombi: Pytam, bo nie ogarniam jeszcze tych sposobów.
30 kwi 23:34

 Może akurat będę wiedziała
Może akurat będę wiedziała 
 tylko nie ciagi ani zbiory bo w tamtych ksiazkach to
chyab kosmos
tylko nie ciagi ani zbiory bo w tamtych ksiazkach to
chyab kosmos 

 zaraz policze
zaraz policze

 Bo moje to duuużo proporcji, głównie Tales i ciężko to przenieść
na forum, więc jakbyś miał jakiś elegancki pomysł, to chętniebym zobaczyła
Bo moje to duuużo proporcji, głównie Tales i ciężko to przenieść
na forum, więc jakbyś miał jakiś elegancki pomysł, to chętniebym zobaczyła 

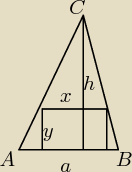


 świetnie rozwiązane zadanie
świetnie rozwiązane zadanie 

 w kazdym razie −
musze sie zastanowic chwile.
w kazdym razie −
musze sie zastanowic chwile.


