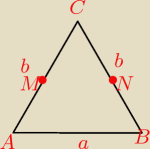
Dany jest trójkąt równoramienny ABC , w którym |AC | = |BC | = b i |AB | = a . Punkty M i N są
rzutami środka podstawy AB trójkąta na ramiona BC i AC . Wyraź pole czworokąta ABMN za pomocą
a i b .
Co to jest rzut środka podstawy? czy to są te punkty co zaznaczyłem? i ABMN to trapez o
ramieniu b/2 ?
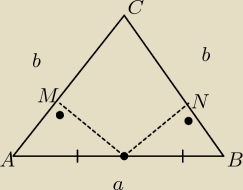zdecydowanie ramieniem nie jest b/2. jak na rysunku, rzut jest to odcinek pod kątem prostym.
ADM = BDN
∡MAD = α = ∡NBD ⇒ ∡ADM=∡BDN=90−α ⇒∡MDN = 2α ?
Pole ABMN to suma pól 2xADM+MDN
AD = 1/2a
Teraz potrzebuje do szczescia tylko dlugosc wyrazic a lub b, tak?
A α z twierdzenia cosinusów?
Pole trapezu ABMN obliczyć jako różnicę pól trójkątów ABC i NMC . Co więcej, trójkąt NMC jest
podobny do trójkąta ABC i dość łatwo jest obliczyć skalę k tego podobieństwa. Z podobieństwa
trójkątów prostokątnych ADC i DNC mamy
| CD | CA | CD2 | h2 |
| 4b2−a2 | ||||||||||||||||
= | ==> CN= | = | = | = | |||||||||||||||||
| CN | CD | CA | b | b | 4b |
| CN | 4b2−a2 | |||
k= | = | |||
| CA | 4b2 |
| 4b2−a2 | ||
PΔNMC=k2PΔABC=( | )2 PABC | |
| 4b2 |
| 4b2−a2 | ||
Pabmn=PΔABC−PΔNMC=PABC − ( | )2 PABC | |
| 4b2 |
| 1 | ||
zostały rachunki tylko MOżna wyłączyć PABC i póżniej za PABC podstawić żePABC = | ah | |
| 2 |
