Okręgi Atar1x: Wyznacz równanie okręgu o promieniu 7/5 , który przechodzi przez punkty wspólne okręgów o równaniach x² − 4x + y² + 2y + 4 = 0 i x² − 4x + y² + 12y + 19 = 0 .

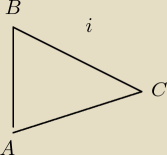
Michał: znajdz punkty wspólne okręgów (A i B) następnie stwórz trójkąt ABC gdzie C− środek szukanego

	7		7
okręgu i mamy że BC to		oraz AC to		. Wyznaczamy prostą AB i szukamy środka odc
	5		5

AB. Prowadzimy prostą prostopadłą do AB przez jej środek.ABC jest równoramienny wiec C należy do utworzonej prostej. Teraz szukamy na tej prostej punktu odległego od A i B o nasz promień. Troche liczenia jest w tym zadaniu ale powinno wszystko wyjść. PS to i na rysunku to przypadek

Atar1x: Po przyrównaniu mam y=⁻³₂ a po podstawieniu tego do pierwszego równania wychodzą chore wartosci dla x np. ^4−√3₂. Co robię nie tak?

Eta:

	4−√3
A niby czemu ... liczba		ma być "chora" ?
	2

Liczba, jak liczba ... i taka właśnie ma być!

Michał: @Eta nam maturzystom jak wychodzi coś takiego to jest czarna rozpacz i szukanie błędu chociaz nie koniecznie on jest jakieś głupie przekonania panuje

Eta:

Michał:

	√3		−3
@Atar1x liczby ci wychodzą dobre ten punkt A to będzie (2−		,		)
	2		2

Atar1x: No właśnie jak wychodzi takie coś to zapala się lampka "coś jest źle" dobra lecę dalej z tym.

Michał: te pierwiastki później "poznikają" i wyjdą w miare spoko ułamki

Atar1x: środek AB (√3,0) y=ax+b ^4−√3₂=⁻³₂a+b 0=a√3+b z tego b i dalej wyliczyc a i b, potem prostopadła do niej?

Michał: jesli szukasz prostopadłej i masz prostą AB to współczynnik kierunkowy też znajdziesz do niej i wyznaczysz b

Michał: ale AB jest równoległy do OX wiec środkowa AB to x=2

Atar1x: równanie prostej prostopadłej y=^9−√3₃₀x−^3√3−1₁₀. Coś pomieszałem?

Atar1x: a nie powinno mi wyjsc x=√3. zgłupiałem...

Mila: x² − 4x + y² + 2y + 4 = 0 (x−2)²−4+(y+1)²−1+4=0 (x−2)²+(y+1)²=1 postać kanoniczna x² − 4x + y² + 12y + 19 = 0 ⇔(x−2)²−4+(y+6)²−36+19=0 (x−2)²+(y+6)²=21 r=√21 Masz dwa punkty:

	√3		−3
A=(2−		,		)
	2		2

	√3		−3
B=(2+		,		)
	2		2

	7
R=
	5

	49
(x−a)2+(y−b)2=
	25

	√3		49
(2−		−a)2+(−1,5−b)2=
	2		25

	√3		49
(2+2		+a)2+(−1,5)2=
	2		25

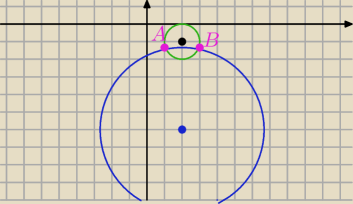
Wiemy, że środek okręgu leży na symetralnej cięciwy AB, x=2 stąd a=2⇔

	√3		49		√3		49
(2−		−2)2+(−1,5−b)2=		⇔(−		)2+(−1,5−b)2=
	2		25		2		25

	√3		49		√3		49
(2+		−2)2+(−1,5−b)2=		⇔(		)2+(−1,5−b)2=
	2		25		2		25

	√3		49		3		9		24
(−		)2+(−1,5−b)2=		⇔		+		+3b+b2=1
	2		25		4		4		25

	21
b2+3b+		=0
	25

	121
Δ=
	25

b₁=−13 lub b₂=4 środki okręgów (2,4), (2,−13) Równania:

	49
(x−2)2+(y−4)2=
	25

	49
(x−2)2+(y+13)2=
	25

niestety nie mieści się rysunek

Atar1x: Dzięki Mila

Mila:

Szkodnik: Niestety rozwiązanie Mili jest błędne. Pierwsza współrzędna środka okręgu jest okey a=2, ale druga juz jest kompletnie z d*py.

	7
13 + 4 >> 2 *
	5

Powinno byc:

	26
b2 + 3b +		= 0
	25

√Δ = 2,2 czyli ostatecznie b₁=−2,6 lub b₂=−0,4 i teraz rozwiązanie ma sens bo 2,6 − 0,4 = 2,2 czyli < 2 * r