jakis pomysł kk: P( A suma B')=0,2 wykaz ze P( A' suma B)≥0,8

M:

bezendu: P(A∪B ′)+P(A′∪B)=P(Ω)=1 dalej już prosto

wredulus_pospolitus: bezendu −−− a od kiedy taka równość zachodzi

bezendu: wredulus a nie zachodzi?

wredulus_pospolitus: P(A) = 0.3 ; P(B) = 0.8 P(A'uB) = 0.8 ; P(AuB') = 1 P(A'uB) + P(AuB') = 1.8 > 1 = P(Ω) Zauważ, że P(A'uB) + P(AuB') = P(A') + P(B) + P(A) + P(B') − P(A'nB) − P(AnB') = = 2 − (P(B) − P(AnB)) − (P(B') − P(A'nB') = 1 + P(AnB) + P(A'nB') więc równość zachodzi tylko gdy P(AnB) = 0 i P(A'nB') = 0 (czyli gdy P(A) + P(B) = 1)

wredulus_pospolitus: Tfu ... oczywiście P(AuB') = 0.3

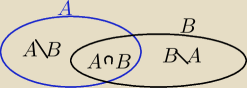
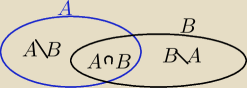NN: A∪B^'≥A i A^'∪B≥A^' to P(A)≤P(A∪B^')=0,2 i P(A^'∪B)≥1−P(A) ≥1−0,2= 0,8