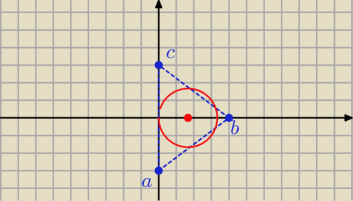
Matura to Bzdura ??!??!?? Kipic: Grube zadanko na mature Wyznacz rownanie okregu wpisanego w trojkat o wierzcholkach A=(0;−3) B(4;0) C(0;3) Ja robie to na skroty bo z rysunku odczytuje ze y rownania tego okregu wynosi 0 a potem podstawiam do wzoru na rownanie okregu dwie styczne Ale to bez sensu bo gdyby nie lezal srodek okregu na osi x to nie umialbym zrobic A jak to fachowo zrobi co do czego Z góry dzięki za pomoc

pigor: SZYBCIEJ

Kipic: @pigor co szybciej Pomoże ktos

Patryk: (x−r)²+y²=r² r−łatwo wyliczyć

Kipic: nie ogarniam co to x co t o y wogule nie ogarniam tego wzoru skad on jest

Patryk: podstawowy wzór na równanie okręgu https://matematykaszkolna.pl/strona/1468.html

Patryk: rozwiązujesz takie zadania z zielonej książki ?

Anka: r łatwo policzyć oblicz długośći boków trójkąta ze wzoru na dl odcinka to jest Δrownoramienny, jak nie rownoboczny, oblicz wysokość BO (O−poczatek ukladu wspolrzednych

	1
Oblicz pole ze wzoru P=		ah
	2

	a+b+c
Potem podstawiasz do wzoru P=		*r i obliczasz r
	2

a dalej jakos pojdzie

123: A nie można ułożyć układu 3 równan krozystając z tych 3 punktów i wzoru na okrąg? Na necie jest pdoobne rozwiązane wlasnie w ten sposob.

Anka:

	1		2
Jak Δ jest rownoboczny to wysokosci dziela sie na odcinki o dł		h i		h wiec srodek
	3		3

okregu obliczysz z wektorow

bżdonc: @Anka, równoramienny

Anka: hmm, to z wektorow nie pojdzie.

123: Kipic, masz do tego odpowiedź?

Anka: Wiem, środek ma wwpolrzedne S(a,b)=S(a,0). Pkt (0,0) na pewno nalezy do okręgu. Podstawić promień, b=0 i pkt (0,0) i chyba wyjdzie a

Anka: Podstawic do wzoru (x−a)²+(y−b)²=r²

Lola: hmm, dziwne to, bo wychodzi mi, że pole to 6 czyli promien to bedzie 12/13? czyli podstawiamy do wwzoru (x−a)²+y²=¹⁴⁴₁₆₉ stąd jeżeli punkt (0,0) należy do okręgu to wychodzi że a=¹²₁₃ lub − ¹²₁₃

Artur_z_miasta_Neptuna: pole wynosi 12 tego trójkąta (patrz rysunek)

Lola: A no sorki

Artur_z_miasta_Neptuna: a zadanie można na wiele sposobów zrobić przykład 'nietypowego' podejścia (nie znaczy że najłatwiejsze i najszybsze) krok 1 rysunek krok 2 zaznaczenie trójkątów prostokątnych którzy przyprostokątna to promień okręgu, przeciwprostokątna to odległość środka okręgu od wierzchołka krok 3 zauważenie, że: każdy z tych trójkątów dzieli kąt wyjściowy (trójkąta równoramiennego) na pół krok 4

	h		4
tgα =		=
	3		3

	α		r
tg		=
	2		3

korzystasz z odpowiednich wzorów aby wyznaczyć r mając wartość tgα

Kipic: Dzieki Dzieki promien wychodzi 1,5 wiec x=1,5

123: A gdyby tak obliczyć pole z wierzchołków a później promień ze wzoru P=pr ? Tutaj widac ze srodek lezy na osi OX to latwo ze wzoru na odleglosc(ktora jest promieniem) punktu od prostej liczymy srodek. Jezeli srodek by nie lezal na osi OX to chyba wystarczy zauwazyc ze |AB|=|BC| wiec wysokosc dzieli podstawe na pol, w ten sposob wyznaczamy rownanie prostej na ktorej lezy srodek. Dobre rozumowanie?

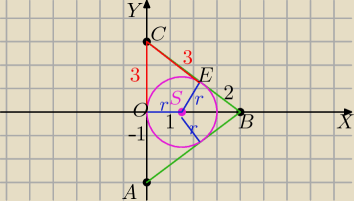
Mila: S=(a,b) − środek okręgu Równanie okręgu (x−a)²+(y−b)²=r² (postać kanoniczna) ΔABC− Δ równoramienny O− punkt styczności okręgu z bokiem AC BC=AB=5 OC=CE=3− punkty styczności okręgu wpisanego w kąt są równo oddalone od wierzchołka kąta.

	2		4		3
ΔSEB∼ΔCOB⇔		=		⇔r=
	r		3		2

	3		3
Równanie okręgu dla a=		, b=0, r=
	2		2

	3		3
(x−		)2+y2=(		)2⇔
	2		2

	3		9
(x−		)2+y2=
	2		4

r można obliczyc z wzoru P_Δ=p*r, p − polowa obwodu Δ

asdf: liczysz długość |AC|, punkt D − to środek odcinka |AC|, później prowadzisz prostą przechodzącą przez środek D i B, na konco korzystasz z tych własności: http://matematyka.opracowania.pl/gimnazjum/okr%C4%85g_opisany_i_wpisany_w_tr%C3%B3jk%C4%85t_r%C3%B3wnoboczny/ i na koniec pokombinować ze wzorami z linki i gotowe

asdf: prostą przechodzącą przez punkty D i B.

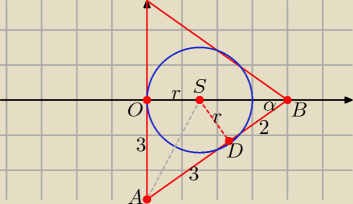
Bogdan: Środek okręgu S = (r, 0), r − długość promienia, |AB| = 5

	3		r		3
Z podobieństwa trójkątów ABO i SBD:		=		⇒ r =
	4		2		2

	3		9
Równanie okręgu: (x −		)2 + y2 =
	2		4

pigor: ..., o , to nie ja , tylko jakiś kretyn(ka) podszył(a) się pod mój nick − post z 16.26

Bogdan: I dlatego pigor warto zarejestrować swój nick