napisz równanie symetralnej odcinka AB, jeśli A= (-3, 6), B=(-3, -4) lena: napisz równanie symetralnej odcinka AB, jeśli A= (−3, 6), B=(−3, −4)

Kipic: liczysz najpierw srodek odcinka AB czyli C potem rownanie prostej kierunkowej AB z y=a₁x +b potem gdy juz masz rownanie prostej kierunkowej AB to zeby pliczyc rownanie prostej prostopadlej to mamy wzor na wspolczynnik kierunkowy tej prostej prostopadlej ze wzoru a₁ *a₂=−1 liczysz a₂ i jest to wspolczynnik kierunkowy tej prostej prostpadlej szukanej podstawiasz pod y=a₂x+b punkt C czyli srodek AB i masz b i zapisujesz rownanie tej prostej prostopadlej przechodzacej przez srodek AB czyli szukanej prostej symetalnej

ania128: A=(−2;−3) B=(−4;−5)

Bogdan: Nie potrzebne jest równanie prostej zawierającej punkty A i B, wystarczy współczynnik kierunkowy tego równania prostej

pigor: ..., lub np. tak : środek AB punkt S=(¹₂(−3−3), ¹₂(6−4))= (−3,1) a wektor AB= [−3+3,−4−6]= [0,−9]= −[0.9] , zatem 0(x+3)+9(y−1)=0 ⇔ y−1=0 ⇔ y=1 . ...

5-latek: Czescpigor Postac kierunkowa prostej jest tak zakorzeniona w swiadomosci uczniow ze nawet Jakub nie podaje tego rozwiazania na tej stronie . Moim zdaniem wielka szkoda .

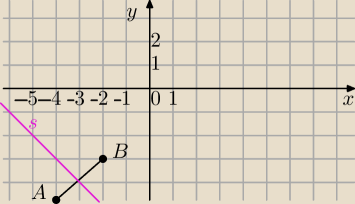
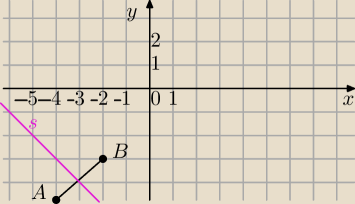Mila: A=(−2;−3) B=(−4;−5) Symetralna odcinka AB jest zbiorem wszystkich punktów jednakowo odległych od końców odcinka P(x,y) dowolny punkt symetralnej √x+2)²+(y+3)²=√(x+4)²+(y+5)² ^2 i wykonuję działania pod pierwiastkami x²+4x+4+y²+6y+9=x²+8x+16+y²+10y+25 4x+6y+13=8x+10y+16+25 −4y=4x+28 s: y=−x−7