Monotoniczność funkcji Blaven: Witam, Czy byłby ktoś na tyle łaskaw, aby mi ktoś wytłumaczyć w sposób prosty, jak policzyć monotoniczność funkcji: y=x−(1/x). Policzyłem już granicę tej funkcji, jej pochodną, a nawet asymptotę ukośną i pionową, ale z monotonicznością nie daję rady. Z góry dziękuje.

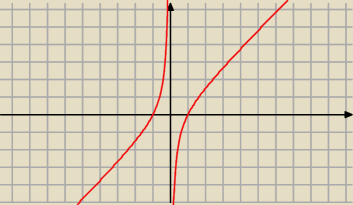
Aga1.: Tak wygląda wykres funkcji. Rozwiąż nierówność f^'(x)>0 Powinno wyjść f^'(x)>0 ⇔x∊R/{0} Na tej podstawie piszesz odpowiedź. f↗dla x∊(−∞,0) oraz x∊(0,∞)

Blaven: Samą odpowiedź znam, dzięki stronie WolphramAlpha. Problemem jest pochodna, która wynosi 1+(1/x²). Nie wiem, jak przyrównać to do zera.

Eta:

	1
1+		≠0
	x2

Blaven: No właśnie i co w takim wypadku?

Aga1.: Widzę,że dla x∊R\{0} f^'(x)>0

Blaven: Coś stworzyłem. Dziękuję za pomoc.