wielomiany dzielenie pankracy: Wielomian w(x)=x⁴+x²−(a−1)x+b jest podzielny przez x²−1 znajdz reszte z dzielenia przez dwumian x−2.

pankracy: jak dla mnie b=−4 i a=3 więc wychodzi na to, że reszta 12, ale odpowiedź jest ponoć zła...

pankracy: błąd u mnie czy w odpowiedzi?

jikA: U Ciebie.

pankracy: rachunkowy czy w rozumowaniu? stworzyłem układ równań w(−1)=0 i w(1)=1 wyliczyłem b i a, a następnie podstawiłem pod x w funkcji w(x) dwójkę.

pankracy: w(1)=0*

pankracy: hop

jikA: A niby dlaczego W(1) = 1?

pankracy: sprostowałem wyzej i tak tez obliczyłem. ktoś wie gdzie jest błąd?

123: Jaka ma byc odpowiedz?

pankracy: test interaktywny, podaje te odpowiedz i mowi ze jest zle.

123: Mi wyszlo a=1, b=−2 i reszta 18

Tomek: mi wychodzi ze

	5
b=−
	2

	1
a=
	2

czyli W(2)=18,5 ale czy to jest dobrze

pankracy: też źle

123: Daj link do tego testu xD

Dziabong: a=1, b = −2 a reszta z dzielenia przez dwumian (x−2) to 18. Czyli albo źle przepisałeś przykład albo zła odpowiedź jest.

pankracy: 18 pasuje

Prosiałke: Dołączę się do liczenia.

Prosiałke: a=1 b=−2 reszta z dzielenia wielomianu w przez (x−2) to 18

pankracy:

	|x|−1
ale teraz troche inny problem ile miejsc zerowych ma funkcja f(x)=		=0
	|x|+2

Dziabong: D = R, |x|−1 = 0 |x|= 1 x= 1 v x = −1

tttt:

	−3
f(x)=		+1
	|x|+2

|x|+2=3 ⇒x=1 vx=−1 <kolega wyzej wpadl na lepszy pomysl >

pankracy: okej, to tez wyszło, ale pominąłem "określona dla rzeczywistych" bo taka odp też była a rozumiem, że to dotyczy dziedziny

tttt: jasne ze dziedzina

pankracy: dobra, teraz troche z innej beczki 8sin⁴x−14sin²+5=0

	1		−1
wyszedł mi sinx=		v sinx=		i co z tym dalej zrobic?
	4		4

pankracy:

	1		1
ops bzdura sin2x=		zatem sinx=		i ujemny, dalej już wiem
	√2		√2

pankracy: jedna druga sin w kwadracie*

Dziabong:

	√2		√2
Dokładnie, wyjdzie sinx =		i sinx = −		, a to są już podstawowe wartości
	2		2

więc nie powinno być problemów.

pankracy: ile miejsc zerowych ma funkcja f(x)=sinx−x²+1 ?

pankracy: ktoś ma jakiś pomysł? bo póki co widzę tylko sinx=(x−1)(x+1) ale chyba niewiele to wnosi

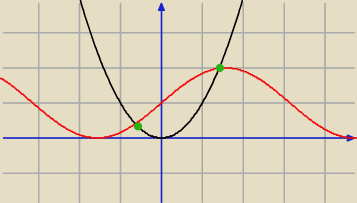
jikA: sin(x) − x² + 1 = 0 sin(x) + 1 = x² Z rysunku zauważamy że te dwie funkcje przecinają się nam w dwóch miejscach.