Oblicz pole figury ograniczonej wykresami funkcji: Muihay:

⎧	f(x)=−2 dla x<4
⎩	f(x)=x−6 dla x≥4

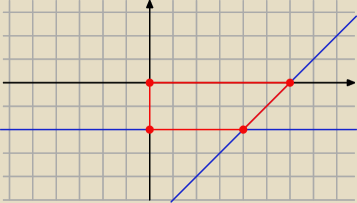
vitek1980: Jeśli figura ma być ograniczona tylko wykresami funkcji to ma nieskończone pole. Może czegoś brakuje w treści? Np. ograniczenia przez osie układu? Wówczas będzie to trapez prostokątny jak na rysunku.

Muihay: Treść zadania nie jest dla mnie jasna, ponieważ dostałem tylko to co napisałem wcześniej oraz "oraz ¹₃x−⁴₃

Muihay: Zdawało mi się, że to jest błąd − pochodzi z innego zadania itp., ale w razie czego podałem

Muihay: Forma zadania wygląda tak: ⎧f(x)=−2 dla x<4 ⎩f(x)=x−6 dla x≥4 oraz ¹₃x−⁴₃ I jeszcze prośba − mógłbyś wytłumaczyć jak konkretnie oblicza się dane wykresy, by nanieść je na układ? Z góry dziękuje

vitek1980: co rozumiesz pod pojęciem "jak oblicza się dane wykresy"? jak masz wzory podane to wykres można sporządzić na podstawie np. tabelki tylko w tym przypadku trzeba pamiętać, że funkcja ma 2 różne wzory. dla x<4 wzór to f(x)=−2 − funkcja stała dla x≥4 f(x)=x−6 funkcja liniowa rosnąca

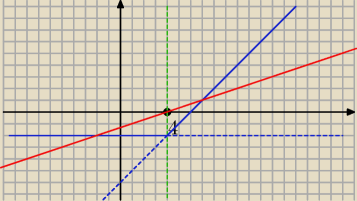
vitek1980: wygląda to mniej więcej tak. Zielona linia wyznacza miejsce "zmiany" wzoru funkcji f ze stałej w rosnącą

	1		4
Czerwonym dorysowałem tę nową funkcję co dopisałeś czyli y=		x−
	3		3

Szukana figura to trójkąt rozwartokątny Odczytaj potrzebne dane: podstawę i wysokość no i masz pole