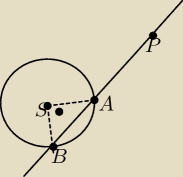
 Z punktu P poprowadzono sieczną okręgu o środku S i promieniu długości 5.
Wiedząc, że |PB|=12 i |PS|=11 oblicz długość cięciwy AB.
−−−−−−
Mi wychodzi że skoro r=5 (dorysowałem r) oraz środek wierzchołkiem trójkąta. To mamy trójkąt
prostokątny równoramienny. Co daje nam |AB|= 5√2
W odpowiedziach mam jednak że |AB|=4
Proszę o pomoc
Z punktu P poprowadzono sieczną okręgu o środku S i promieniu długości 5.
Wiedząc, że |PB|=12 i |PS|=11 oblicz długość cięciwy AB.
−−−−−−
Mi wychodzi że skoro r=5 (dorysowałem r) oraz środek wierzchołkiem trójkąta. To mamy trójkąt
prostokątny równoramienny. Co daje nam |AB|= 5√2
W odpowiedziach mam jednak że |AB|=4
Proszę o pomoc
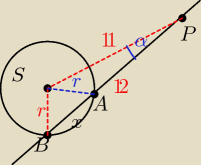 tam nie ma kata prostego
tam nie ma kata prostego  !
najlepiej z twierdzenia kosinusów obliczyć kąt α:
ΔBPS:
25=144+121−2*11*12cosα
!
najlepiej z twierdzenia kosinusów obliczyć kąt α:
ΔBPS:
25=144+121−2*11*12cosα
| 10 | ||
cosα= | ||
| 11 |
| 10 | ||
25=121+(12−x)2−2*11*(12−x)* | ||
| 11 |
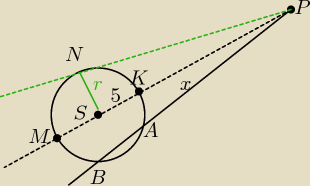 Masz zastosować twierdzenie o stycznej i siecznej.
Dlaczego zaznaczyłaś kąt prosty między promieniami?
NP − styczna
|NP|2=|MP|*|PK|
|NP|2=|BP|*|AP|⇔
16*6=12*x
x=8
|AB|=4
Masz zastosować twierdzenie o stycznej i siecznej.
Dlaczego zaznaczyłaś kąt prosty między promieniami?
NP − styczna
|NP|2=|MP|*|PK|
|NP|2=|BP|*|AP|⇔
16*6=12*x
x=8
|AB|=4