Podaj argumenty dla których funkcja f(x)=x^2+2x-3 przyjmuje wartosci nie mniejsz Madzik: Podaj argumenty dla których funkcja f(x)=x²+2x−3 przyjmuje wartosci nie mniejsze od funkcji g(x)=−x²+2x−1

asdf: x² + 2x − 3 >= −x² + 2x − 1

Madzik: a jeśli nie mniejsze to nie powinno być ≥ ? i później z tego Δ obliczyć i x₁ i x₂ , tak?

Madzik: haluuu

ICSP: >= jest innym oznaczeniem ≥

Tomek: tak tez jest zapisane tylko zamiast ≥ dał >= i z tego wynika ze 2x²−2≥0

Madzik: i teraz wyliczyć x₁ i x₂ ?

Licealista_Theosh: I zapisz przedział kiedy 2x²−2 jest nad osią OX.

123: Jak chcesz to mozesz, ale latwiej ze wzoru skroconego mnozenia

Licealista_Theosh: a nie lepiej 2 przed nawias?

Madzik: i wychodzi x₁≥1 i x₂≥−1 ? i co teraz, jakis przedział trzeba , czy to juz wszystko?

123: No 2 przed nawias a później ze wzoru skróconego mnożenia

Licealista_Theosh: x₁ i x₂ to punkty a nie przedziały.

Madzik: ale nie mozna powiedziec, np ze argumenty w przedziale od ≤1;∞) i ≤−1;∞) , bo nie wiem w koncu jaka jest odpowiedz jak to zapisac, te argumenty nie mniejsze

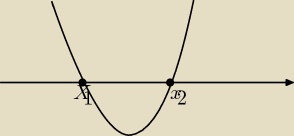
Tomek: x₁=−1 x₂=1 x∊(−∞, −1>∪<1, +∞) f(x)≥g(x) <=> x∊(−∞, −1>∪<1, +∞)

Madzik: no okej, jako postaram to ogranac