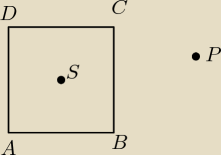
dowód miśka: Dany jest kwadrat ABCD o środku w punkcie S i punkt P − jak na rysunku. Udowodnij, ze suma kwadratów odległości punktu P od wierzchołków A,B,C i D jest równa 4|PS|² + |AC|².

M:

M:

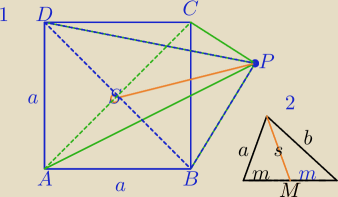Mila: 1) środkowa Δ: rys. 2 a²+b²=2s²+2m² PS jest środkową ΔBDP oraz środkową ΔACP. 2) |AC|²=(a√2)²=2a² Z wzoru na środkową Δ: ΔACP:

	a√2
|CP|2+|AP|2=2|PS|2+2*(		)2
	2

(*) |CP|²+|AP|²=2|PS|²+a² ΔBDP:

	a√2
|DP|2+|BD|2=2|PS|2+2*(		)2
	2

(**)|DP|²+|BD|²=2|PS|²+a² ====================== 3) (*)+(**) 4|PS|²+2a²=|AP|²+|BP|²+|CP|²+|DP|² |AP|²+|BP|²+|CP|²+|DP|²=4|PS|²+|AC|² ==============================