oblicz cosinusy kątów w tym trójkącie oraz jego pole karo: W trójkącie ABC : IABI = 2 cm, IBCI = ^√3₂ cm, IACI = 1,5 cm. oblicz cosinusy kątów w tym trójkącie oraz jego pole NIE używając wzorów : P = ¹₂ a * b * sin γ P = √p(p−a)(p−b)(p−c) P = ¹₂ a^{2 sinβ * sinγ}_sinα

MałyMatematyk: Z twierdzenia cosinusów.

KAMIL: Cosinusy z twierdzenia cosinusów https://matematykaszkolna.pl/strona/543.html.

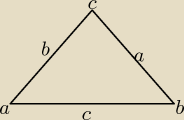
MałyMatematyk: Analogicznie do każdego kąta: a²= b²+c²−2bc cosA

Bogdan:

	9
x2 + h2 =
	4

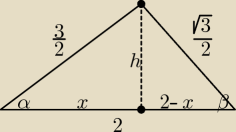
	3		3		9		3
(2 − x)2 + h2 =		⇒ 4 − 4x + x2 + h2 =		⇒ 4 − 4x +		=
	4		4		4		4

itd.

karo: to z twierdzenia cosinusów też można obliczyć pole?

Bogdan:

	1
Oblicz x, potem h, pole P =		*2*h
	2

olaf: