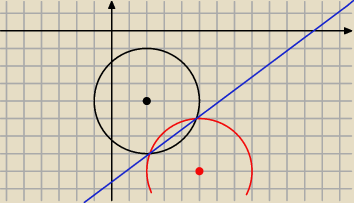
Okrąg o równaniu (x-2)^2 + (y+4)^2 = 9 przesunięto o wektor u[3,-4]. bangzi: Okrąg o równaniu (x−2)² + (y+4)² = 9 przesunięto o wektor u[3,−4]. a)Znajdź równanie obrazu tego okręgo w przesunięciu równoległym o wektor u. b)Wyznacz równanie osi symetrii figury będącej sumą obu okręgów pomoże mi ktoś rozwiązać to zadanie? zupełnie nie wiem jak mam sie zabrać do tego

aniabb: obraz (x−5)² + (y+8)²=9 oś symetrii y=3/4 x − 69/8

bangzi: a mogłabyś powiedzieć jak ci to wyszło? Podpunkt a) wiem jak zrobiłaś, ale z osią już nie

aniabb: prostopadła do odcinka utworzonego z środków okręgów przechodząca przez środek tego odcinka

bangzi: no tak <facepalm> dziękuje

bangzi: sorry że zawracam głowe ale wynikiem b) powinno być y=−4/3x−4/3 ; y=3/4x−69/8 nie mam pojęcia czemu powinny wyjść 2 wyniki oraz jak obliczyć żeby wyszły dwa, bardzo prosze o wytłumaczenie

aniabb: zapominam że to ma 2 osie symetrii ;> prosta łącząca środki też jest osią symetrii