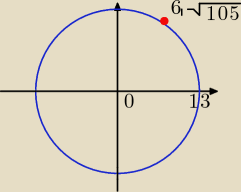
Kto mi może pomóc :P plissss Patiiiiiiiiiii: Sprawdź rachunkowo , czy dany punkt należy do okręgu o środku w początku układu współrzędnych i promieniu 13.

krystek: wstaw i licz x²+y²=13²

NIKOLCIAAA: no to mi pomóż pliska

Patiiiiiii: no ale nie wiem co potem

krystek: za x=.. y=..

Patiiiiiii: czyli poprosu nie możesz mi pomóc prosze

krystek: jeżeli dobrze odczytałam to (6)²+(√105)²=13²

Prosiałke: (6,√105) x y

Prosiałke: x= 6 y=√105

Patiiiiiii: czyli jak to będzie bo nie wiem jak mam to zapisać ?

Krzysiek : Patrz co napisala Krystek o 20.17 . Tak to masz zapisac i policzyc czy to jest prawda Jesli tak to nalezy jesli nie to nie nalezy A treraz napisze to co Pan/i od matematyki napewno mowil/a na lekcji Rownaniie okregu w postaci kanonicznej wyglada tak (x−x_s)²+(y−y_s)²=r² Wspolrzedne x_s i y_s to wspolrzedne srodka okregu u nas to (0,0 ) bo srodek lezy w poczatku ukladu wspolrzednych . Wiec x_s=0 i y_s=0 Teraz jesli jakis punky nalezy do wykresu funkcji to oznacza ze misi spelniac to rownanie . Nasz punkt ma wspolrzedne (6,√105} WSpolrzedna x tego punktu to 6 czyli x=6 , a wspolrzedna y to √105 czyli y=√105 . OProcz tego masz podane wzadaniu ze promien r=13 . Masz juz wszystkie dane zeby sprawdzic czy ten punkt nalezy do tego okregu (x−x_s)²+(y−y_s)²=13² wie \c podstawiamy dane (6−0)²+(√105−0)²=13² to dostaniemy 6²+√105²=13² Teraz widzisz skad sie wzial zapis Krystek \ Obliczenia zrob sobie sama . TO juz bardzo latwe jest