Funkcja bezendu: Funkcja f określona jest wzorem f(x)=x²+x+1. Znajdź wzór funkcji g, której wykres otrzymamy: a) przesuwając wykres funkcji f wzdłuż osi OY o 2 jednostki do dołu f(x)−2 f(x)−2=x²+x+1−2=x²+x−1 b) przesuwając wykres funkcji wzdłuż osi OX o 2 jednostki w prawo f(x−2) f(x−2)=(x−2)²+(x−2)+1 f(x−2)=x²−4x+4+x−2+1 f(x−2)=x²−3x+3 c) przekształcając wykres funkcji f w symetrii względem osi OY i tu mam problem wiem tyle,że jak względem osi OY to −f(x) Może ktoś dać jakąś wskazówkę

Prosiałke: Cała funkcja w nawiasie, a przed nią minus. Chociaż nie jestem pewien, ale tak mi się wydaje.

Prosiałke: Chyba tak. Na 85% JESTEM PEWIEN.

bezendu: @Prosiałke źle napisałem jak względem osi OY to f(−x)

Prosiałke: Sprawdzę dla Ciebie.

Prosiałke: f(−x) to symetria względem osi OY

Krzysiek : http://pl.wikibooks.org/wiki/Matematyka_dla_liceum/Funkcje_i_ich_w%C5%82asno%C5%9Bci/Przekszta%C5%82canie_wykresu_funkcji zobacz tutaj

bezendu: Dziękuje za link czyli za x podstawić −x f(−x)=(−x)²+(−x)+1=x²−x+1

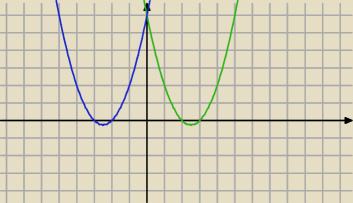
Mila: c) f(−x) względem OY Przykład f(x)= x²−5x+6 f(−x)=(−x)²+5x+6

bezendu: a teraz względem początku punktu (0,0) −f(−x)=−[(−x)²+(−x)+1]=−(x²−x+1)=−x²+x−1 ok

bezendu: Mila jak byś miała chwilkę to sprawdź czy zapis jest poprawny bo po co tracić punkty i jeszcze taki podpunkt: przesuwając wykres funkcji f o wektor [−1,−3], a następnie otrzymany wykres przekształcając w symetrii względem osi OY czyli najpierw przesuniecie o wektor f(x+1)−3 f(x+1)−3=(x+1)²+(x+1)+1−3 x²+2x+1+x+1−2 x²+3x teraz względem osi OY f(−x)=(−x)²+3(−x)=x²−3x ok

Eta: ok

bezendu: @Eta a sprawdzisz zapis pozostałych

Prosiałke: Eta, mógłbym Cie prosić o pomoc w zadaniu?

Mila: Eta szybka, jak błyskawica.

bezendu: Jeszcze mam takie jedno zadanko: W wyniku jakich przekształceń lub przekształcenia wykresu funkcji f(x)=x²+3x można otrzymać wykres funkcji g,jeżeli a) g(x)=(x−5)⁴+3(x−5)−5 przekształcenie f(x+5)−5 czy lepiej napisać przesunięcie o wektor [5,−5] b) g(x)=x⁴−3x przekształcenie symetrii względem osi OY f(−x) c) g(x)=|x⁴+3x+1| czyli |f(x)+1| d) g(x)=−x⁴+3x tutaj nie wiem

bezendu: już wiem −f(−x) oczywiście pomyłka wzór funkcji f(x) wygląda tak x⁴+3x

Mila: a) translacja o wektor [5,−5] i otrzymujemy wzór: f(x−5)−5

bezendu: czyli wersja z wektorem

bezendu: a pozostałe są ok

Mila: c) translacja o wektor [0,1], symetria względem OX , tej części wykresu, która leży pod osią OX (y<0)

bezendu: czyli mój zapis jest błędny dziękuje Mila

Mila: Nie jest błędny, ale mniej dokładny.

bezendu: Niestety nie wiem jak jest w odpowiedziach,ponieważ zbiór mam od kserowany bez odpowiedzi ale na pewno jest tak jak napisałaś Jeszcze raz dziękuje i miłego wieczoru