Symetralna odcinka AB. demostenes: Witam, nie mogę się uporać z jednym zadaniem, mimo kilku godzin analizowania wszystkich lekcji, materiałów z podręcznika itp. Mam takie zadanie: Wyznacz równanie symetralnej odcinka AB, korzystając ze wzoru na odległość między punktami. A(1,8) B(5,4) Wiem tyle, że trzeba obliczyć prostą AB i środkową S, ale co dalej? Jak zrobić symetralną odcinka?

demostenes: Bardzo proszę o pomoc.

Dziabong: Musisz wyznaczyć prostą prostopadła przechodząca przez środek tego odcinka Aby była prostopadła musi spełniać warunek a₁ x a₂ = −1

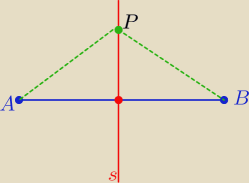
Eta: Każdy punkt należący do symetralnej s odcinka AB jest równo odległy od końców tego odcinka. P(x,y) |AP|= |BP| ⇒ |AB|²= |BP|² (x−1)²+(y−8)²= (x−5)²+(y−4)² dokończ...... otrzymasz równanie symetralnej s: y= x+3

PW: _→ Równanie prostej prostopadłej do wektora AB przechodzącej przez punkt S. Jeżeli koniecznie korzystając ze wzoru na odległość, to: symetralna ma taką własność, że każdy jej punkt jest jednakowo oddalony od A i od B, czyli zapisujemy to jako |PA| = |PB|, gdzie P=(x,y). Po skorzystaniu ze wzoru na odległość punktów dostaniesz równanie symetralnej.