Wykres funkcji wymiernej z dwoma wartosciami bezwzglednymi nieudolny1: Jak sobie poradzic z narysowaniem takich wykresów fukcji?

	x
a) f(x)=|		|
	x−1

	|x+1|
b) f(x)=
	|x|−1

	1
O ile jeszcze w podpunkcie a) wiem że trzeba rozpisać licznik i wyjdzie (chyba?) f(x)=|
	x

+ 1|, tak nie wiem jak mam ruszyć te wartości bezwględne w podpunkcie b)

nieudolny1:

	1
w a) f(x)=|		+1| jednak
	x−1

Prosiałke: Jeśli cała funkcja jest w wartości bezwzględnej to: Rysujesz normalnie funkcje i obijasz na drugą mańkę to co jest pod wykresem OX nad oś OX. Zaś gdy jest wartość bezwzględna przy x to, to co jest po prawej stronie dajesz na lewą.

Dziabong:

	1
W podpunkcie a) rysujesz najpierw funkcję		, następnie przesuwasz o wektor [1,1], a potem
	x

wszystko to co pod osią OX rysujesz nad nią

Prosiałke: Ewentualnie zawsze możesz sobie rozpisać i badać funkcje. Spróbuj w b) Rozpisujesz dla |x+1|: x+1 dla x≥−1 −x−1 dla x<−1 Teraz dla |x|: x dla x≥0 −x dla x<0 Tworzysz przedziały. Powstaną 4 i 4 przypadki badasz, gdy x jest takie i takie.

Dziabong: Pamiętaj jeszcze o dziedzinach.

nieudolny1: Więc mam 4 przypadki:

	x+1		2
1* f(x)=		=>		+1
	x−1		x−1

	x+1
2* f(x)=		=> −1
	−x−1

	−x−1
3* f(x)=		− tu nie wiem co z tym, bo w odpowiedziach nie ma takiej opcji
	x−1

	−x−1
4* f(x)=		=> 1
	−x−1

Więc teraz to wszystko narysować na osi i będzie dobrze?

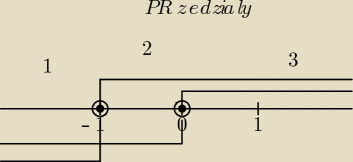
Prosiałke: Ehhhh...− 1) x∊(−∞,−1) postawiasz wartość −x+1 i −x do funkcji Później sprawdzasz z ustaloną dziedziną. 2) x∊<−1,0) podstaw wartości x+1 i −x do funkcji Później sprawdzasz z ustaloną dziedziną. 3) x∊<0,∞) podstaw wartości x+1 i x do funkcji Obliczasz f(x) w takich przedziałach. I rysujesz wykresy w podanych przedziałach

Prosiałke: Nie zapomnij oznaczyć pusta kulką liczby wyrzuconej z dziedziny na wykresie.

Prosiałke: Jak czegoś nie rozumiesz to pytaj.

nieudolny1: Ok, to ogarnąłem już te przedziały, nie wiem dokładnie jak mam je sprawdzić z dziedziną i skąd odczytać asymptoty dla wykresu

nieudolny1: Up

nieudolny1: Ok, już nie trzeba pomocy, doszedłem do tego sam