dla jakich wartości a równanie |x^2-4|=a ma dokładnie trzy rozwiazania Madzik: dla jakich wartości a równanie |x²−4|=a ma dokładnie trzy rozwiazania

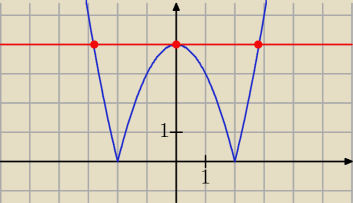
Bogdan: y = |x² − 4| y = a

Dominik: dla a = 4 narysuj f(x) = |x² − 4| i odczytaj z wykresu

Madzik: A można to jakoś zapisać, tzn. chodzi mi o obliczenia ?

PW: Tu nie potrzeba obliczeń. Powołujemy się na "znane własności funkcji kwadratowe". Rozpatrywana funkcja f jest dla x∊(−∞,−2)∪(2,∞) tożsama z funkcją kwadratową g(x)=x²−4. Z własności funkcji kwadratowej wiemy zatem, że jest ona: − malejąca na przedziale (−∞,−2) − rosnąca na przedziale (2,∞) i przyjmuje na tych przedziałach wartości od 0 do ∞. Dla a>0 istnieją więc 2 pierwiastki równania g(x)=a. Rozpatrywana funkcja f jest na przedziale <−2,2> tożsama z funkcją h(x)=−x²+4. wiemy zatem, że: − przyjmuje wartość 0 dla x₁=−2 i dla x₂=2 − jest rosnąca na przedziale <−2,) i malejąca na przedziale (0,2> − w punkcie x₀=0 osiąga maksimum równe 4. Dla a∊<0,4) równanie h(x)=a ma więc 2 pierwiastki, a dla a=4 − jeden pierwiastek. Dla pozostałych a pierwiastków nie ma. Podsumowanie: równanie f(x)=a ma 3 pierwiastki dla a=4. Bogdan po prostu narysował streszczenie tego ględzenia (które nic nie wnosi do zrozumienia sensu), i to wystarczy − nikt więcej od ucznia nie wymaga oprócz tego, żeby napisał, że z własności funkcji kwadratowej wynika, iż wykres funkcji f ma przebieg jak na rysunku, a więc 3 rozwiązania są dla a=4.