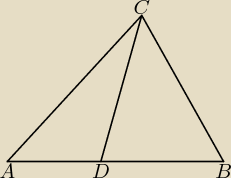
 Dwusieczna CD dzieli trójkąt ABC na trójkąty ADC i CDB, których stosunek pól jest równy 2:3.
Zatem:
A. |AD| : |AB|= 2:5
B. |AD| : |AB| = 4 : 25
C. |AD| : |DB| = 4:9
D. |AD| : |DB| = √2 : √3
Dwusieczna CD dzieli trójkąt ABC na trójkąty ADC i CDB, których stosunek pól jest równy 2:3.
Zatem:
A. |AD| : |AB|= 2:5
B. |AD| : |AB| = 4 : 25
C. |AD| : |DB| = 4:9
D. |AD| : |DB| = √2 : √3
| P1 | 2 | ||
= | |||
| P2 | 3 |
| 2 | 12|AD|*h | ||
= | |||
| 3 | 12|DB|*h |
| 3 | ||
|DB| = | |AD| | |
| 2 |
| 5 | ||
|AB| = |AD| + |DB| = | |AD| | |
| 2 |
| |AB| | 5 | ||
= | |||
| |AD| | 2 |
