Sprawdzi ktoś? chodzi o punkty na maturze, czy dostałbym maxa?
allleksander:
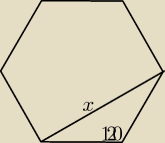
≈Proszę o sprawdzenie zapisu zadania emotka Oblicz parwdopodob, że dwa losowo wybrane
wierzchołki sześciokąta foremnego o boku długości 1 są końcami odcinka o długości √3.
Narysowałem sześcian, wypisalem wszystkie ary wierzchołków które mają dl √3, x obliczyłem z tw
cos, takich wierzchołków jest 6 i to jest moje zdarzenie A, którego bd obliczal
prawdopodobieństwo, Ω=6(bo 6 ścian)+6(bo 6 par takich wierzchołków jest z mojego zdarzenia
A)+3(dłuższe przekątne) czyli wynik moc zdarzenia A=2/5 ok?2
PW: Przestrzeń zdarzeń elementarnych Ω to zbiór wszystkich dwuelementowych podzbiorów zbioru
6−elementowego. Z treści zadania wynika, że każdy wybór jest jednakowo prawdopodobny, mozna
więc zastosować twierdzenie zwane klasyczną definicją prawdopodobieństwa:
Niech A oznacza zdarzenie "wylosowano wierzchołki odległe o
√3"
A={{A
1,A
3}, {A
2,A
4}, {A
3,A
5}, {A
4,A
6}, {A
5,A
1}, {A
6,A
2}
|A| = 6.
Dowód, że wszystkie wymienione dwójki wierzchołków są odległe o
√3 wynika z twierdzenia
cosinusów (patrz rysunek). Wiadomo, że kąty sześciokąta foremnego mają miary 120°, a więc
x
2=1
2+1
2−2•1•1•cos120°
x
2=2−2cos120°
x
2=2−2cos(90°+30°)
x
2=2+2sin30°
x
2=3,
a więc x=
√3, bo x>0. Nietrudno zauważyć, że przy wyborze innych dwóch wierzchołków ich
odległość będzie równa 2 lub równa 1.
Zgodnie z (1)
Jest mi miło, że nie obraziłeś się na surową krytykę.. Trochę się wytłumaczę. Jest to zadanie z
rachunku prawdopodobieństwa. Elementarz to ustalenie przestrzeni zdarzeń elementarnych Ω i
określenie, w jaki sposób jest na niej zdefiniowane prawdopodobieństwo (w tym wypadku
przywołanie klasycznej definicji prawdopodobieństwa).
Bez tego nie ma punktów na
egzaminie. Reszta (twierdzenie cosinusów do ustalenia, które wierzchołki są oddalone o
√3)
to tylko zabawa. Grozę egzaminatora musi zaś budzić wypowiedź (cytuję):
Ω=6(bo 6 ścian)+6(bo 6 par takich wierzchołków jest z mojego zdarzenia
A)+3(dłuższe przekątne) czyli wynik moc zdarzenia A=2/5.
Już napisanie Ω=6 właściwie dyskwalifikuje rozwiązanie, a "moc zdarzenia A=2/5" dobija. Widać,
że wiesz o co idzie, ale język matematyczny szwankuje.
Życzę wytrwałości, a ja muszę marudzić w imię poszanowania języka (jestem już stary i bardziej
cenię jasność wypowiedzi niż znajomość jakiegoś twierdzenia).
