zagubiony: Proszę o wskazówki!
W trójkącie ABC bo AC jest o 6 cm dłuższy od boku AB, a |BC|=5
√2.
Wiedząc, że kąt ABC = 135stopni, oblicz promień okręgu opisanego na tym trójkącie.
Odpowiedź jest 13
√2 : 2
Błagam o pomoc


27 kwi 17:16
bysztszak: wskazówka pierwsza:
ogórkiem się nie ogolisz
27 kwi 17:18
madam66:
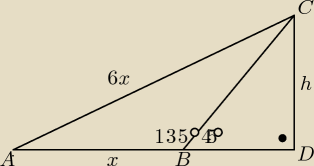
R− promien kola opisanego
R=1/2*AC
BC=5√2
wiec z wlasnosci trojkata 45 45 i 90 h=5 i BD=5
teraz masz takie rownanie z twierdzenia pitagorasa:
6x [do kwadratu]= 5[kwardat] + (5+x) [kwadrat]
do tego doszłam ale nie wiem czy jest dobrze, nie moge wiecej pomóc musze leciec
27 kwi 17:51
bysztszak: czekaj, przepisuje rozwiązanie na komputer
27 kwi 18:13
bysztszak:
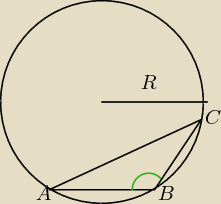
|BC}=5
√2
|AB|=x
|AC|=x+6
z tw. cosinusów:
(x+6)
2=x
2+(5
√2)
2−2*x*5
√2*cos135
| | √2 | |
x2+12x+36=x2+50−10*x*√2*(− |
| ) |
| | 2 | |
x
2 się redukuje
12x+36=50+10x
2x=14 ⇒ x=7
teraz twierdzenie:
R=7
√2
BOOOOOOOOOOOYAAAAAAAAAAH
27 kwi 18:29
bysztszak:

|BC}=5
√2
|AB|=x
|AC|=x+6
z tw. cosinusów:
(x+6)
2=x
2+(5
√2)
2−2*x*5
√2*cos135
| | √2 | |
x2+12x+36=x2+50−10*x*√2*(− |
| ) |
| | 2 | |
x
2 się redukuje
12x+36=50+10x
2x=14 ⇒ x=7
teraz twierdzenie:
R=7
√2
BOOOOOOOOOOOYAAAAAAAAAAH
27 kwi 18:29
10Pionio: Pozwolę sobie zauważyć, że do wzoru
R={a}{2sinα}
podstawiamy a=13, nie 7!
28 kwi 04:25


 R− promien kola opisanego
R=1/2*AC
BC=5√2
wiec z wlasnosci trojkata 45 45 i 90 h=5 i BD=5
teraz masz takie rownanie z twierdzenia pitagorasa:
6x [do kwadratu]= 5[kwardat] + (5+x) [kwadrat]
do tego doszłam ale nie wiem czy jest dobrze, nie moge wiecej pomóc musze leciec
R− promien kola opisanego
R=1/2*AC
BC=5√2
wiec z wlasnosci trojkata 45 45 i 90 h=5 i BD=5
teraz masz takie rownanie z twierdzenia pitagorasa:
6x [do kwadratu]= 5[kwardat] + (5+x) [kwadrat]
do tego doszłam ale nie wiem czy jest dobrze, nie moge wiecej pomóc musze leciec
 |BC}=5√2
|AB|=x
|AC|=x+6
|BC}=5√2
|AB|=x
|AC|=x+6
 |BC}=5√2
|AB|=x
|AC|=x+6
|BC}=5√2
|AB|=x
|AC|=x+6