twierdzenie sinusów Ups: 1. Wyznacz pole trójkąta, mając daną długość jednego z jego boków oraz miary dwóch kątów do niego przyległych 2. Oblicz długość promienia okręgu opisanego na trójkącie, w którym a= 2√13 , cos alfa = − √3 / 4 Będę bardzo wdzięczna za pomoc

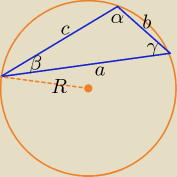
Bogdan: a) dane: a, β, γ. α = 180 − (β + γ) ⇒ sinα = sin(β + γ)

	b		a		1
Z twierdzenia sinusów:		=		⇒ b = ..., pole P =		absinγ
	sinβ		sinα		2

	a
b) Z twierdzenia sinusów:		= 2R R = ...
	sinα

Lore: Wynik zad. 2 to R=4 znam wzór który podałeś, ale nie wiem co zrobić z tym nieszczęsnym cosα

Baju-baj:

	sinβsinγ		2√13
S=0,5a2		; 2R=		;R=4
	sin(β+γ)		(1−316)0,5

rex: jedynka trygonometryczna się kłania