Twierdzenie sinusów. Lore: Mam problem z dwoma zadaniami, oba związane z twierdzeniem sinusów 1. Wyznacz pole trójkąta, mając daną długość jednego z jego boków oraz miary dwóch kątów do niego przyległych 2. Oblicz długość promienia okręgu opisanego na trójkącie, w którym a= 2√13 , cos alfa = − √3 / 4 Będę bardzo wdzięczna za pomoc

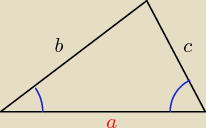
123: Zad 1. Czyli mamy dane: bok a kąty α, β przyległe do tego boku

a		b
	=
sin(180−(α+β))		sinβ

a		b
	=
sin(α+β)		sinβ

a		b
	=
sinαcosβ+cosαsinβ		sinβ

b(sinαcosβ+cosαsinβ)=asinβ

	asinβ
b =
	sinαcosβ+cosαsinβ

	1
P =		absinα
	2

	1		asinβ
P =		a		sinα
	2		sinαcosβ+cosαsinβ

	a2sinαsinβ
P =
	2sinαcosβ+2cosαsinβ

Ja bym to tak zrobił

Lore: dziękuję! zgadza się! tylko dół jest jeszcze sprowadzony do sin(α + β)

123: No tak to można sprowadzić... W ogóle sam siebie nie rozumiem dlaczego rozpisałem wzór na sin(α+β).

Lore: 2. Oblicz długość promienia okręgu opisanego na trójkącie, w którym a= 2√13 , cosα = − √3 / 4 A to tutaj?

Lore: Dobra, dałam radę, nieważne!

PW: Zadanie 1. Jeżeli oznaczymy długość danego boku symbolem a, zaś miary kątów do niego przyległych symbolami β i γ, to lezący naprzeciw a kąt α ma miarę 180°−(β+γ). Z twierdzenia sinusów

	a
		=2R
	sinα

	a
		=2R,
	sin(180°−(β+γ))

po zastosowaniu wzoru redukcyjnego

	a
(1)		=2R,
	sin(β+γ)

gdzie R oznacza promień okręgu opisanego na trójkącie. Podobnie z twierdzenia sinusów (2) b=2Rsinβ (3) c=2Rsinγ. Podstawiając równość (1) do (2) i (3) otrzymamy

	a
b=		sinβ
	sin(β+γ)

	a
c=		sinγ
	sin(β+γ)

Pole P trójkąta obliczamy stosując wzór

	1
P=		absinγ,
	2

czyli

	1		a		a2sinβsinγ
P=		a		sinβsinγ=		,
	2		sin(β+γ)		2sin(β+γ)

jak widać liczenie c, czyli wzór (3) można pominąć − nie było to potrzebne do rozwiązania

	1
zadania (aczkolwiek można zastosować wzór P=		acsinβ) − wynik oczywiście będzie ten sam,
	2

a można pominąć liczenie b).

PW: Lore, nie odświeżałem, więc wykonałem kawał dobrej, nikomu nie potrzebnej roboty, ale wynik mamy ten sam, to i tak dobrze. Pozdrawiam.

Lore: Zdarza się, że ktoś zdąży przed drugą osobą, prawda? A co do zadania drugiego: po porostu poszukałam głębiej w internecie i znalazłam podobny typ zadania na zupełnie innych liczbach.

Lore: W każdym razie i tak bardzo dziękuję i pozdrawiam