Dominik: | | x | |
nalezy udowodnic, ze zbiorem wartosci f(x) = |
| jest y∊ℛ dla x∊ℛ{−2, 2}. jakies |
| | 4 − x2 | |
pomysly?
26 kwi 22:36
jikA:
Może coś takiego
| x | | −(2 − x) + 2 | | 2 | |
| = |
| = |
| − 1. |
| (2 − x)(2 + x) | | (2 − x)(2 + x) | | x + 2 | |
26 kwi 22:43
Eta:
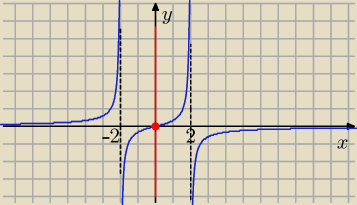
26 kwi 22:53
Dominik: wydawalo mi sie, ze nie da rady podzielic wielomianu stopnia pierwszego przez wielomian stopnia
drugiego, a tu pare przeksztalcen i jest ladna postac kanoniczna. dzieki

26 kwi 22:54
Dominik: Eta, myslisz ze cos takiego licealista jest w stanie narysowac?

26 kwi 22:55
Dominik: zaraz zaraz, ale czy ten wykres nie przeczy troche funkcji, ktora skonstrulowal jiikA?
26 kwi 22:57
jikA:
| | 2 | |
W wyrażeniu |
| − 1 należy pamiętać jeszcze że do dziedziny nie należy liczba x = 2. |
| | x + 2 | |
26 kwi 23:05
asdf: zeby umiec to narysowac musisz znać takie rzeczy jak:
asymptoty pionowe, ukosne (czyli granice funkcji), monotonicznosc (pierwsza pochodna),
wkleslosc/wypuklosc (druga pochodna).
26 kwi 23:08
Dominik: wiem, rysowala mi podobna funkcje znajoma. ja sie nie mam co w takie rzeczy bawic − zadanie
jest ze zbioru dla licealistow, wiec licealista powinien umiec je zrobic w inny sposob.
26 kwi 23:11
Dominik: | | 2 | |
aczkolwiek wciaz mnie dziwi ten wykres − nie odpowiada on funkcji |
| − 1 |
| | x + 2 | |
26 kwi 23:11
Eta:
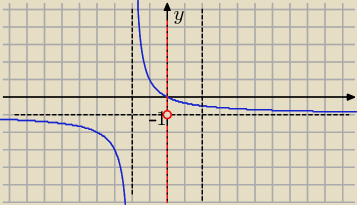
| | 2 | |
y = |
| −1 ZW= R\{−1}  |
| | x+2 | |
26 kwi 23:11
Dominik: wiem jak wyglada wykres tej funkcji.

diametralnie sie rozni od twojego poprzedniego wykresu,
mimo ze to ta sama funkcja. gdzie tu logika?
26 kwi 23:19
pigor: ..., no to jeszcze np. tak:
| | x | |
y= |
| /*(4−x2) i x≠±2 ⇒ 4y−yx2= x ix∊R\{−2,2} ⇒ |
| | 4−x2 | |
⇒
yx2+x−4y=0 − równanie kwadratowe zmiennej x, które ma rozwiązanie ⇔
⇔ Δ ≥0 ⇔ 1
2+4y*4y ≥0 ⇔ 4y
2+1 ≥0 ⇔
y∊R −szukany zbiór wartości funkcji f. .

26 kwi 23:22
Eta:

26 kwi 23:24
Dominik: dzieki pigor, to chyba najbardziej do mnie przemawia.

poza tym, wyjasni mi ktos te roznice
wykresow tej samej funkcji?
26 kwi 23:31
pigor: ..., niestety
jika nie miał prawa skracać tak jak to zrobił

,a więc "jego" wzór
nie jest równoważny danej funkcji , czyli jej wykres nie powinien cię interesować . ...

26 kwi 23:38
Eta:
Dokładnie

26 kwi 23:39
asdf: moze funkcje wielomianowe da się w inny sposób narysować, gorzej jest z funkcjami, gdzie jest
postać potęgowa lub logarytmiczna, np.
f(x) = e−x2 * ln(1−x)
dlatego Ci napisalem ogolnie co jest potrzebne do narysowania tego...
26 kwi 23:39
Dominik: a czemuz to nie wolno tak skracac? gdzie jest blad?
26 kwi 23:39
pigor: | | a±b | | a | | b | | 1 | | b | |
... , bo skraca się tak : |
| = |
| ± |
| = |
| ± |
| . ...  |
| | ac | | ac | | ac | | c | | ac | |
26 kwi 23:46
26 kwi 23:47
Dominik: no przeciez! dzieki wielkie pigor!
26 kwi 23:47
Dominik: w ogole dzieki wielkie wszystkim udzielajacym sie.

26 kwi 23:48
jikA:
Ponieważ to jest funkcja a nie równanie więc nie można tak sobie upraszać.
Przykład masz funkcję kwadratową
f(x) = 3x2 + 6x + 3 więc można sobie niby podzielić przez 3 i mamy f(x) = x2 + 2x + 1
dla x = 0 nasza pierwsza funkcja przyjmuje wartość 3 natomiast druga 1 i a więc funkcja
ta nie jest równoważna wyjściowej.
26 kwi 23:49
asdf: też przy niektorych wyrazeniach trzeba uważać ze skracaniem i pamiętać o dziedzinie, np.
g(x) = 1
D
f ≠ D
g ≠ D
h
26 kwi 23:49
asdf: albo taki częsty popełniany błąd:
| 2−x | | 2−x | | √2−x | |
| = |
| = |
| |
| √4−x2 | | √(2+x)(2−x) | | √2+x | |
no a to juz jest źle...
26 kwi 23:54





 diametralnie sie rozni od twojego poprzedniego wykresu,
mimo ze to ta sama funkcja. gdzie tu logika?
diametralnie sie rozni od twojego poprzedniego wykresu,
mimo ze to ta sama funkcja. gdzie tu logika?


 poza tym, wyjasni mi ktos te roznice
wykresow tej samej funkcji?
poza tym, wyjasni mi ktos te roznice
wykresow tej samej funkcji?
 ,a więc "jego" wzór
nie jest równoważny danej funkcji , czyli jej wykres nie powinien cię interesować . ...
,a więc "jego" wzór
nie jest równoważny danej funkcji , czyli jej wykres nie powinien cię interesować . ... 


