dlugosc krzywej slaw: Dlugosc krzywej. Witam! Mam do policzenia dlugosc krzywej: y=lnsinx, dla x∊(pi/3,pi/2) i nie mogę tego wyliczyc. Nie mogę przejsc na calke oznaczona, gdyz w pewnym momencie utykam na całce 1/sinx dx. I teraz moje pytanko, czy cos gdzies po drodze za bardzo skracam i wychodzi mi ta trudna calka do policzenia, czy cos zle licze czy mozna wyciagnac z tego jakas inna postac? a moze taki trudny przyklad to jest z taka trudna calka? Jezeli komus chcialoby sie to przeliczyc, bylbym wdzieczny. Pozdrawiam!

Krzysiek: aby policzyć tą całkę skorzystaj z podstawienia uniwersalnego: http://pl.wikipedia.org/wiki/To%C5%BCsamo%C5%9Bci_trygonometryczne#Funkcje_trygonometryczne_wyra.C5.BCone_przy_pomocy_tangensa_po.C5.82owy_k.C4.85ta t=tgx/2 albo pomnóż licznik i mianownik przez sinx, a następnie podstawienie: t=cosx

slaw: super, skorzystam chyba z drugiego sposobu. Podstawieniem uniwersalnym robilem ale mi wychodza tangensy w logarytmach. a ze to calka oznaczona to klopotliwa bedzie to policzenia, wole jakas prostsza wersje tej funkcji To mam jeszcze pytanko. Mam policzyc dlugosc takiej krzywej: http://www.wolframalpha.com/input/?i=y+%3D+arcsinx+%2B+%281-x^2%29^%281%2F2%29+ i licze i ładnie wychodzi mi wynik 4. , natomiast w odpowiedziach mam wynik pi. I teraz ja licze dobrze czy dobre sa odpowiedzi?

Krzysiek: nie wiem w jakich granicach jeżeli tak jak wpisałem do wolframa i wolfram dobrze liczy(interpretuje to co napisałem) to wychodzi 4.

slaw: w granicach −1,2. a moglbys podac linka? To sie przy okazji naucze wpisywac dlugosci do wolframu Aha co do pierwszej calki. pomnozylem *sinx/sinx, mianownika zamienilem na 1−cos²x, podstawilem za t = cosx i dostalem calke − arcsinx(cosx) , czy dobrze?

slaw: dobra, z tym sinusem to zle policzylem, bo mi sie wzory pomylily. Pokaz mi tylko tego linka, jezeli mozesz Pozdrawiam!

Krzysiek: może i jest jakaś funkcja w wolframie która liczy długość funkcji ja jej nie znam więc 'normalnie' wpisuję: http://www.wolframalpha.com/input/?i=integral_%28-1%29%5E%281%29+sqrt%281%2B%28%28arcsinx+%2B+%281-x%5E2%29%5E%281%2F2%29+%29%27%29%5E2%29 nie może być w granicach [−1,2]...

	−dt
po podstawieniu dostajesz taką całkę: ∫
	1−t2

slaw: od −1,1 w granicah co wynika z dziedziny. Piatek dzis a ja siedze nad matma i stad te glupiutki bledy chyba

slaw: co do pierwszej calki. policzylem i wyszlo mi dobrze aleee, jak wstawie granice calkowania to logarytm wychodzi z zera, a to nieskonczonosc, calka niewlasciwa. a ma byc ladna z wynikiem 2pi.

Krzysiek: a o jakiej całce teraz piszesz?

slaw: o tej z sinusem. w sensie o tym zadanku pierwszym co wstawilem. mam policzyc dlugosc tej krzywej lnsinx w granicach co podalem powyzej. zatrzymalem sie tam w pewnym momencie na calce 1/sinx. teraz udalo mi sie ja policzyc dzieki Twojej pomocy. Natomiast jak juz to zrobilem to jak wstawiam granice, niestety wychodzi mi logarytm naturalny z 0.

Krzysiek: nic takiego nie wychodzi, co najwyżej podstawiając pi/2 dostajemy 1/2ln1=0

slaw:

	cosx − 1
calka z 1/sinusx wychodzi 1/2ln|		| , prawda?
	cosx + 1

Krzysiek: też mi tak wyszło.

slaw: to wynika z tego, ze mam cos chyba z kalkulatorem. Bo jak wpisuje do niego cos(pi/2) to mi pokazuje 1. a to przeciez w rzeczywistosci jest 0. niewiem czemu taki blad robi

Mila:

	π
a=
	3

	π
b=
	2

	1		x
a∫b		=ln(tg		)]ab=
	sinx		2

	π		π
=ln(tg		)− ln(tg		)=
	4		6

	√3		1		1
=ln(1)−ln(		)=0−ln(√3)+ln(3)=ln(3)−		ln(3)=		ln(3)
	3		2		2

http://www.wolframalpha.com/input/?i=y%3Dlnsinx%2C+pi%2F3%3Cx%3Cpi%2F2 Ta krzywa w podanych granicach nie może mieć długości 2π. Może cos przekręciłeś w zadaniu?

slaw: dzieki MIla. tak, twoja odpowiedz jest dobra. Ja zle przeczytalem. Sluchaj a moze doradzisz mi jak rozwalic pole powierzchniy bryly obrotowej: y = 1/(x−1) dla x∊(2,4) ?

Mila: Pomyślę.

slaw: chodzi mi o to, ze w pewnym momencie mam taka sytuacje:

	1		1
∫		√(1 +		) dx i niewiem jak z tego wyjsc...
	x−1		(x−1)4

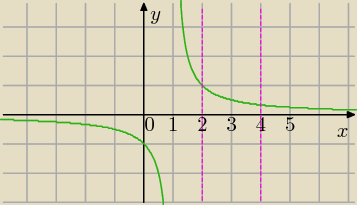
Mila: Na pewno powierzchnię , nie objętość?

slaw: powierzchnie , ale bryly obrotowej. czyli ten dluzszy wzor z 2pi. Tak napewno

Mila:

	1
y=f(x)=
	x−1

	−1
f'(x)=
	(x−1)2

a=2 b=4

	1		1
S=2πa∫b		√1+		dx=
	x−1		(x−1)4

	1		(x−1)4+1
=2π∫		*(		)1/2 dx=
	(x−1)		(x−1)4

	√(x−1)4+1		(x−1)4+1
=2π∫		=2π∫		dx rozbijamy na dwie całki
	(x−1)3		(x−1)3√(x−1)4+1

	(x−1)4		1
=2π*(∫		dx+∫		dx)=
	(x−1)3√(x−1)4+1		(x−1)3√(x−1)4+1

	x−1		1
2π(∫		dx+∫		dx)
	√(x−1)4+1		(x−1)3√(x−1)4+1

teraz licz w pierwszej podstawienie: (x−1)²=t w drugiej podstawienie:

1
	=t
x−1

slaw: istny kosmos Ale dzieki

Mila: Tak, to "pracowita" całka, mam nadzieję, że już Ci wyjdzie, bo sporo pisania.

krzysiek: A propo tej długości krzywej. Wynik obliczenia innym sposobem różni się od tego podanego wyżej. Prosiłbym o znalezienie błędu. ∫√1+ctg²xdx=∫√¹_sin²xdx=∫¹_sinxdx granice początkowo od pi/3 do pi/2. podstawiam t=cosx zmieniam granice na od 1/2 do ^√2₂ (czy dobrze?) dostaje całke ∫¹_t²−1dt=1/2ln|^t−1_t+1| podstawiam granice 1/2ln3+1/2 ln|(^√2₂−1)/(^√2₂+1)| a to na pewno nie jest równe 1/2ln3