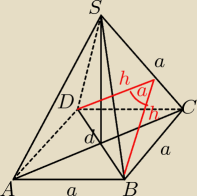
Wszystkie krawędzie ostrosłupa prawidłowego czworokątnego mają tę samą długość. Oblicz cosinus
kąta między sąsiednimi ścianami bocznymi.
d=a√2
Z cosinusów:
2a2= 2h2 − 2h2cosα
2a2=2h2(1 − cosα) /: 2h2
| 2a2 | ||
1 − cosα = | ||
| 2h2 |
| a2 | ||
cosα = 1 − | ||
| h2 |
| a√3 | ||
h= | ||
| 2 |
