Funkcja bezendu: Naszkicuj wykres funkcji g, która każdej wartości parametru m∊<−5,7> przyporządkowuje liczbę rozwiązań równania f(x)=m

Mila: Nie widzę funkcji f(x).

bezendu: Takie jest polecenie na potwierdzenie zadanie 3.15 zbiór Andrzeja Kiełbasy poziom pods+roz podpunkt o)

Mila: Owszem, jest polecenie i jest wykres. Patrz na wykres (I) Zaczynamy od dołu:( rysujesz poziomą linię i patrzysz w ilu punktach przecina wykres funkcji) 1) dla m∊<−5,−4) 0 rozwiązań 2) m∊<−4,−2) 1 rozw. 3) m=−2 2 rozw. 4) m∊(−2,3) 3 rozw. 5) m∊<3,4) 4 rozw 6) m=4 3 rozw. 7) m∊(4,6) 2 rozw 8) m=6 1 rozw. 9) m∊(6,7> 0 rozw. Narysujesz wykres? Sprawdź w Twojej książce, bo może jest zmiana w treści w innym wydaniu.

bezendu: Dziękuje za odpowiedź

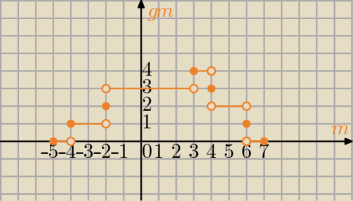
Mila: g(m)=0 dla m∊<−5,4) g(m)=1 dla m∊<−4,−2) g(m)=2 dla m=−2 g(m)=3 dla m∊(−2,3) g(m)=4 dla m∊<3,4) g(m)=3 dla m=4 g(m)=2 dla m∊(4,6) g(m)=1 dla m=6 g(m)=0 dla m∊(6,7>

bezendu: Mila dziękuje za wykres

Mila: Zrób samodzielnie drugi przykład z tego zadania.

bezendu: ok wszystkie podpunkty

bezendu: a) D_f=<−6,6> b) MZ=(6,0) , (5,0) , (0,0 c) f(4)=5 d) Nie istnieje (kółeczko nie zamalowane ) e) (−4,6> f) (−6,−5)∪(−1,0) g) <−5,−2>∪<0,6> h) ↗ (−6,3) ↘ i f(3)=6 j) dla trzech argumentów k f(0)=0 l (−4,−2)∪(1,5) m) 2 rozwiązania n) 5 rozwiązań wykres zrobię ale to za chwilę

bezendu: 1) m∊<−5,−3) 0 rozwiązań m=−3 2 rozwiązania m∊(−3,0) 2 rozwiązania m=0 3 rozwiązania m∊(0,5) 3 rozwiązania m=5 3 rozwiązania m∊(5,7> 2 rozwiązania zgadza się

Mila: Pożyczyłam książkę, gdy mi zwrócą, to sprawdzę ( dzisiaj, później).

bezendu: Ok

Mila: b) miejsca zerowe : {−5,0,6} nie pisz jako punkty, bo stracisz punkty. (miejsce zerowe to argument dla którego funkcja ma wartość zero) f) u mnie (−6,−5)∪(−2,0) : h) popraw rośnie w przedziałach:(−6,−2> U(−2,3> maleje dla x∊(3,6> l (−4,−2>∪(1,5) Mam inaczej na wykresie II: 1) dla m∊<−5,−4> 0 rozwiązań 2) dla m∊(−4,−3) 1 r 3)dla m∊<−3,0) 2 r 4) dla m∊<0,5> 3 r 5) dla m∊(5,6) 2 r 6) dla m=6 1 r 7) dl m∊(6,7> 0 r

bezendu: Mila u mnie wykres wygląda tak: http://pokazywarka.pl/aqivhs/ poprawiłem te podpunkty które kazałaś f) <−6,5)∪(−2,0) h) ↗ (−6,3) czemu u Ciebie w przedziale 3 jest domknięta ↘ (3,6) l ) (−4,−2)∪(1,5) i tu znowu u Ciebie 2 jest> a to nie powinno być że jeśli większe lub równe to wtedy przedziały <..> a jak są większe albo mniejsze to przedziały (.......)

bezendu: jeszcze takie pytanie jak wyznaczam monotoniczność funkcji to przedziały zamknięte czy otwarte bo w różnych książkach są różne wersje

Mila: JUtro odpowiem.

zombi: W zasadzie, powinno się podawać przedziały otwarte, bo w konkretnym punkcie nie możesz powiedzieć, że funkcja maleje lub rośnie.

Technik: W książkach są różne wersję np Jakub podaje w przedziałach zamkniętych a w podręczniku często możemy spotkać przedział otwarty ja myślę tak jak zombie ale może niech ktoś mądrzejszy się wypowie

Mila: h) Nie możesz napisać, że rośnie w przedziale (−6,3) bo w x=−2 jest "urwisko" x₁=−2, f(−2)=5 , x₂=1, f(1)=3 −2<1 i 5>3 nie jest spełniony warunek wzrostu wartości funkcji, Piszemy ,że funkcja rośnie przedziałami. Jeśli chodzi o domykanie przedziałów, to ja pisałabym otwarte przedziały, ale ostatnio przyjmuje się wersję, że domknięte, o ile końce przedziałów należą do dziedziny. Na pewno piszemy domknięcie, gdy proszą o wskazanie maksymalnego przedziału monotoniczności, pamiętaj o uwzględnieniu dziedziny. Punkt l) f(−4)=3 (otwarty ) f(−2)=5>3 ( domknięty) f(1)=3 (otwarty) f(5)=3 ( otwarty)

bezendu: czyli h)↗ (−6,−2)∪(−2,3) teraz ok

bezendu: wczoraj szukałem na internecie odpowiedzi do tego zadania i w przypadku podpunktu l) przedziały były z każdej strony otwarte..

Mila: Punkt (l) f(−2)=5>3, czyli −2 jest argumentem dla którego wartość funkcji jest większa od 3.

bezendu: ok czyli −2 domknięty dziękuje

Mila: